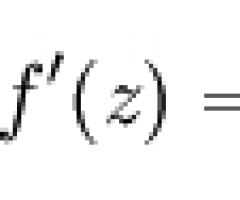Уравнение состояния с запаздыванием. Устойчивость систем с запаздыванием. Уравнения и структура моделей протяженных динамических объектов
ВВЕДЕНИЕ
Министерство образования Российской Федерации
Международный образовательный консорциум «Открытое образование»
Московский государственный университет экономики, статистики и информатики
АНО «Евразийский открытый институт»
Э.А.Геворкян
Дифференциальные уравнения с запаздывающим аргументом
Учебное пособие Руководство по изучению дисциплины
Сборник задач по дисциплине Учебная программа по дисциплине
Москва 2004
Геворкян Э.А. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ: Учебное пособие, руководство по изучению дисциплины, сборник задач по дисциплине, учебная программа по дисциплине / Московский государственный университет экономики, статистики и информатики – М.: 2004. – 79 с.
Геворкян Э.А., 2004
Московский государственный университет экономики, статистики и информатики, 2004
Учебное пособие |
|
Введение................................................................................................................................. |
|
1.1 Классификация дифференциальных уравнений с |
|
отклоняющимся аргументом. Постановка начальной задачи................................................ |
|
1.2 Дифференциальные уравнения с запаздывающим аргументом. Метод шагов. ........ |
|
1.3 Дифференциальные уравнения с разделяющимися |
|
переменными и с запаздывающим аргументом....................................................................... |
|
1.4 Линейные дифференциальные уравнения с запаздывающим аргументом................ |
|
1.5 Дифференциальные уравнения Бернулли с запаздывающим аргументом. ............... |
|
1.6 Дифференциальные уравнения в полных дифференциалах |
|
с запаздывающим аргументом.................................................................................................. |
|
ГЛАВА II. Периодические решения линейных дифференциальных уравнений |
|
с запаздывающим аргументом.................................................................................................. |
|
2.1. Периодические решения линейных однородных дифференциальных уравнений |
|
с постоянными коэффициентами и с запаздывающим аргументом...................................... |
|
2.2. Периодические решения линейных неоднородных дифференциальных |
|
.................. |
|
2.3. Комплексная форма ряда Фурье.................................................................................... |
|
2.4. Отыскание частного периодического решения линейных неоднородных |
|
дифференциальных уравнений с постоянными коэффициентами и запаздывающим |
|
аргументом разложением правой части уравнения в ряд Фурье........................................... |
|
ГЛАВА III. Приближенные методы решения дифференциальных уравнений |
|
с запаздывающим аргументом.................................................................................................. |
|
3.1. Приближенный метод разложения неизвестной функции |
|
с запаздывающим аргументом по степеням запаздывания.................................................... |
|
3.2. Приближенный метод Пуанкаре. .................................................................................. |
|
ГЛАВА IV. Дифференциальные уравнения с запаздывающим аргументом, |
|
появляющемся при решении некоторых экономических задач |
|
с учетом временного лага............................................................................................................... |
4.1. Экономический цикл Колецкого. Дифференциальное уравнение
с запаздывающим аргументом, описывающего изменение
запаса наличного капитала........................................................................................................ |
|
4.2. Характеристическое уравнение. Случай вещественных |
|
корней характеристического уравнения................................................................................... |
|
4.3. Случай комплексных корней характеристического уравнения................................. |
|
4.4. Дифференциальное уравнение с запаздывающим аргументом, |
|
(потребление пропорционально национальному доходу)...................................................... |
|
4.5. Дифференциальное уравнение с запаздывающим аргументом, |
|
описывающего динамику национального дохода в моделях с лагами |
|
(потребление экспоненциально растет с темпом прироста)................................................... |
|
Литература.............................................................................................................................. |
|
Руководство по изучению дисциплины |
|
2. Перечень основных тем..................................................................................................... |
|
2.1. Тема 1. Основные понятия и определения. Классификация |
|
дифференциальных уравнений с отклоняющимся аргументом. |
|
Дифференциальные уравнения с запаздывающим аргументом. ........................................... |
|
2.2. Тема 2. Постановка начальной задачи. Метод шагов решения |
|
дифференциальных уравнений с запаздывающим аргументом. Примеры........................... |
|
2.3. Тема 3. Дифференциальные уравнения с разделяющимися |
|
переменными и с запаздывающим аргументов. Примеры. .................................................... |
|
2.4. Тема 4. Линейные дифференциальные уравнения |
|
2.5. Тема 5. Дифференциальные уравнения Бернулли |
|
с запаздывающим аргументом. Примеры. ............................................................................... |
|
2.6. Тема 6. Дифференциальные уравнения в полных дифференциалах |
|
с запаздывающим аргументом. Необходимые и достаточные условия. Примеры.............. |
|
2.7. Тема 7. Периодические решения линейных однородных дифференциальных |
|
уравнений с постоянными коэффициентами и с запаздывающим аргументом. |
|
2.8. Тема 8. Периодические решения линейных неоднородных дифференциальных |
|
уравнений с постоянными коэффициентами и с запаздывающим аргументом. |
|
Примеры. ..................................................................................................................................... |
|
2.9. Тема 9. Комплексная форма ряда Фурье. Отыскание частного периодического |
|
решения линейных неоднородных уравнений с постоянными коэффициентами и с |
|
запаздывающим аргументом разложением правой части уравнения в ряд Фурье. |
|
Примеры. ..................................................................................................................................... |
|
2.10. Тема 10. Приближенное решение дифференциальных уравнений с |
|
запаздывающим аргументом методом разложения функции от запаздывания |
|
по степеням запаздывания. Примеры....................................................................................... |
|
2.11. Тема 11. Приближенный метод Пуанкаре нахождения периодического |
|
решения квазилинейных дифференциальных уравнений с малым параметром и |
|
с запаздывающим аргументом. Примеры. ............................................................................... |
2.12. Тема 12. Экономический цикл Колецкого. Дифференциальное уравнение
с запаздывающим аргументом для функции К(t), показывающей запас наличного
основного капитала в момент t.................................................................................................. |
|
2.13. Тема 13. Анализ характеристического уравнения, отвечающего |
|
дифференциальному уравнению для функции K(t). ............................................................... |
|
2.14. Тема 14. Случай комплексных решений характеристического уравнения |
|
(ρ = α ± ιω ).................................................................................................................................. |
|
2.15. Тема 15. Дифференциальное уравнение для функции у(t), показывающего |
|
функция потребления имеет вид c(t -τ ) = (1 - α ) у (t -τ ), где α - постоянная норма |
|
производственного накопления................................................................................................ |
|
2.16. Тема 16. Дифференциальное уравнение для функции y(t), показывающего |
|
национальный доход в моделях с лагами капитальных вложений при условии, что |
|
функция потребителя имеет вид c (t − τ ) = c (o ) e r (t − τ ) ............................................................... |
|
Сборник задач по дисциплине........................................................................................... |
|
Учебная программа по дисциплине................................................................................. |
|
Учебное пособие
ВВЕДЕНИЕ
Введение
Настоящее учебное пособие посвящено изложению методов интегрирования дифференциальных уравнений с запаздывающим аргументом, встречающихся в некоторых технических и экономических задачах.
Вышеуказанными уравнениями обычно описываются любые процессы с последействием (процессы с запаздыванием, с временной задержкой). Например, когда в исследуемом процессе значение интересующей нас величины в момент времени t зависит от величины x в момент времени t-τ , где τ – временной лаг (y(t)=f). Или, когда значение величины y в момент времени t зависит от значения этой же величины в момент вре-
мени t-τ (y(t)=f).
Процессы, описывающиеся дифференциальными уравнениями с запаздывающим аргументом встречаются и в естественных, и в экономических науках. В последних это связано как с существованием временного лага в большинстве связях цикла общественного производства, так и с наличием инвестиционных лагов (период от начала проектирования объектов до ввода в действие на полную мощность), демографических лагов (период от рождения до вступления в трудоспособный возраст и начала трудовой деятельности после получения образования).
Учет временного лага при решении технических и экономических задач имеет важное значение, так как наличие лага может существенно повлиять на характер получаемых решений (например, при определенных условиях может привести к неустойчивости решений).
С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
ГЛАВА I. Метод шагов решения дифференциальных уравнений
с запаздывающим аргументом
1.1. Классификация дифференциальных уравнений с отклоняющимся аргументом. Постановка начальной задачи
Определение 1 . Дифференциальными уравнениями с отклоняющимся аргументом называются дифференциальные уравнения, в которых неизвестная функция X(t) входит при различных значениях аргумента.
X(t) = f { t, x (t), x } ,
X(t) = f [ t, x (t), x (t - τ 1 ), x (t − τ 2 )] , |
||||
X(t) = f t, x (t), x (t), x [ t -τ (t )] , x [ t − τ |
||||
X(t) = f t, x (t ) , x (t) , x (t/2), x(t/2) . |
||||
(t )] |
||
Определение 2. Дифференциальным уравнением с запаздывающим аргументом называется дифференциальное уравнение с отклоняющимся аргументом, в котором производная наивысшего порядка от неизвестной функции входит при одинаковых значениях аргумента и этот аргумент не меньше, чем все аргументы неизвестной функции и ее производных, входящих в уравнение.
Заметим, что согласно определению 2, уравнения (1) и (3) при условиях τ (t ) ≥ 0 , t − τ (t ) ≥ 0 будут уравнениями с запаздывающим аргументом, уравнение (2) будет уравне-
нием с запаздывающим аргументом, если τ 1 ≥ 0 , τ 2 ≥ 0 , t ≥ τ 1 , t ≥ τ 2 , уравнение (4) есть уравнение с запаздывающим аргументом, так как t ≥ 0 .
Определение 3. Дифференциальным уравнением с опережающим аргументом называется дифференциальное уравнение с отклоняющимся аргументом, в котором производная наивысшего порядка от неизвестной функции входит при одинаковых значениях аргумента и этот аргумент не больше остальных аргументов неизвестной функции и ее производных, входящих в уравнение.
Примеры дифференциальных уравнений с опережающим аргументом:
X (t) =
X (t) =
X (t) =
f { t, x(t), x[ t + τ (t) ] } ,
f [ t , x (t ), x (t + τ 1 ), x (t + τ 2 )] ,
f t , x (t ), x . (t ), x [ t + τ (t )] , x . [ t + τ
(t )] . |
|

I. МЕТОД ШАГОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
Определение 4. Дифференциальные уравнения с отклоняющимся аргументом, не являющиеся уравнениями с запаздывающим или опережающим аргументом называются дифференциальными уравнениями нейтрального типа.
Примеры дифференциальных уравнений с отклоняющимся аргументом нейтрального типа:
X (t) = f t, x(t) , x(t − τ ) , x(t − τ ) |
|||
X (t) = f t, x(t) , x[ t − τ (t) ] , x[ t − τ (t) ] , x[ t − τ (t) ] . |
|||
Отметим, что аналогичная классификация применяется и для систем дифференциальных уравнений с отклоняющимся аргументом заменой слова "функция" словом "вектор функция".
Рассмотрим простейшее дифференциальное уравнение с отклоняющимся аргументом:
X (t) = f [ t, x(t) , x(t − τ ) ] , |
где τ ≥ 0 и t − τ ≥ 0 (фактически рассматриваем дифференциальное уравнение с запаздывающим аргументом). Основная начальная задача при решении уравнения (10) заключается в следующем: определить непрерывное решение X (t ) уравнения (10) для t > t 0 (t 0 –
фиксированное время) при условии, что X (t ) = ϕ 0 (t ) , когда t 0 − τ ≤ t ≤ t 0 , где ϕ 0 (t ) – заданная непрерывная начальная функция. Сегмент [ t 0 − τ , t 0 ] называется начальным множеством, t 0 называется начальной точкой. Предполагается, что X (t 0 + 0) = ϕ 0 (t 0 ) (рис. 1).
X (t ) = ϕ 0 (t)
t 0 − τ |
t 0 + τ |
0 + τ |
||||
Если запаздывание τ |
в уравнении (10) зависит от времени t |
(τ = τ (t )) , то началь- |
||||
ная задача ставится следующим образом: найти решение уравнения (10) при t > t 0 , если известна начальная функция X (t ) = ϕ 0 t при t 0 − τ (t 0 ) ≤ t ≤ t 0 .
Пример. Найти решение уравнения.
X (t) = f [ t, x(t) , x(t − cos 2 t) ] |
||
при t > t 0 = 0 , если начальная функция X (t ) = ϕ 0 (t ) при (t 0 − cos2 t 0 ) | |
t ≤ t0 |
|
t 0 = 0 |
− 1 ≤ t ≤ 0).
I. МЕТОД ШАГОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
Пример. Найти решение уравнения
X (t) = f [ t, x(t) , x(t / 2 ) ] |
при (t |
−t |
/ 2) | |
||||||
t > t 0 = 1 , если начальная функция X (t ) = ϕ t |
≤ t ≤ t |
||||||||
t = 1 |
t = 1 |
||||||||
1/ 2 ≤ t ≤ 1).
Отметим, что начальная функция обычно задается или находится экспериментально (в основном в технических задачах).
1.2. Дифференциальные уравнения с запаздывающим аргументом. Метод шагов
Рассмотрим дифференциальное уравнение с запаздывающим аргументом.
Требуется найти решение уравнения (13) при t ≥ t 0 .
Для нахождения решения уравнения (13) при t ≥ t 0 будем пользоваться методом шагов (метод последовательного интегрирования).
Суть метода шагов состоит в том, что сначала найдем решение уравнения (13) для t 0 ≤ t ≤ t 0 + τ , потом для t 0 + τ ≤ t ≤ t 0 + 2τ и т.д. При этом заметим, например, что так как в области t 0 ≤ t ≤ t 0 + τ аргумент t − τ меняется в пределах t 0 − τ ≤ t − τ ≤ t 0 , то в уравнении
(13) в данной области вместо x (t − τ ) можно взять начальную функцию ϕ 0 (t − τ ) . Тогда
получим, что для нахождения решения уравнения (13) в области t 0 ≤ t ≤ t 0 |
+ τ нужно ре- |
|
шить обыкновенное дифференциальное уравнение без запаздывания в виде: |
||
[ t, x(t) , ϕ 0 (t − τ ) ] , |
||
X (t) = f |
||
при t 0 ≤ t ≤ t 0 + τ |
с начальным условием X (t 0 ) = ϕ (t 0 ) (см. рис. 1). |
|
найдя решение этой начальной задачи в виде X (t ) = ϕ 1 (t ) , |
можем поста- |
|
вить задачу нахождения решения на отрезке t 0 + τ ≤ t ≤ t 0 + 2τ и т.д.
Итак имеем:
0 (t − τ ) ] , |
||||
X (t) = f [ t, x(t) , ϕ |
||||
при t 0 |
≤ t ≤ t0 + τ , X (t0 ) |
= ϕ 0 (t 0 ) , |
||
X (t) = f [ t, x(t) , ϕ 1 (t − τ ) ] , |
||||
при t 0 +τ ≤ t ≤ t 0 + 2 τ , |
X (t 0 + τ ) = ϕ 1(t 0 + τ ) , |
|||
X (t) = f [ t, x(t) , ϕ 2 (t − τ ) ] , |
||||
при t 0 + 2τ ≤ t ≤ t 0 + 3τ , |
X (t 0 + 2 τ ) = ϕ 2 (t 0 + 2 τ ) , |
|||
X (t) = f [ t, x(t) , ϕ n (t − τ ) ] , |
||||
при t 0 + n τ ≤ t ≤ t 0 + (n +1 ) τ , X (t 0 + n τ ) = ϕ n (t 0 + n τ ) , |
||||
ϕ i (t ) есть |
решение рассматриваемой начальной |
задачи на отрезке |
||
t 0 + (i −1 ) τ ≤ t ≤ t 0 +i τ |
(I=1,2,3…n,…). |
|||

I. МЕТОД ШАГОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ЗАПАЗДЫВАЮЩИМ АРГУМЕНТОМ
Такой метод шагов решения дифференциального уравнения с запаздывающим аргументом (13) позволяет определить решение X (t ) на некотором конечном отрезке изменения t.
Пример 1. Методом шагов найти решение дифференциального уравнения 1-го порядка с запаздывающим аргументом
(t) = 6 X (t − 1 ) |
||||
в области 1 ≤ t ≤ 3 , если начальная функция при 0 ≤ t ≤ 1 имеет вид X (t ) = ϕ 0 (t ) = t . |
||||
Решение. Сначала найдем решение уравнения (19) в области 1 ≤ t ≤ 2 . Для этого в |
||||
(19) заменим X (t − 1) на ϕ 0 (t − 1) , т.е. |
||||
X (t − 1 ) = ϕ 0 (t − 1 ) = t| t → t − 1 = t − 1 |
||||
и учтем X (1) = ϕ 0 (1) = t | |
||||
Итак в области 1 ≤ t ≤ 2 получим обыкновенное дифференциальное уравнение вида |
||||
(t )= 6 (t − 1 ) |
||||
или dx (t ) |
6 (t −1 ) . |
|||
Решая его с учетом (20), получим решение уравнения (19) при 1 ≤ t ≤ 2 в виде |
||||
X (t) = 3 t 2 − 6 t + 4 = 3 (t − 1 ) 2 + 1. |
||||
Для нахождения решения в области 2 ≤ t ≤ 3 в уравнении (19) заменим X (t − 1) на |
||||
ϕ 1 (t −1 ) = 3 (t −1 ) 2 +1 | t → t − 1 |
3(t − 2) 2 + 1. Тогда получим обыкновенное |
дифференциальное |
||
уравнение: |
||||
(t ) = 6[ 3(t − 2) 2 + 1] , X (2) = ϕ 1 (2) = 4 , |
||||
решение которого имеет вид (Рис. 2) |
||||
X (t) = 6 (t − 2 ) 3 + 6 t − 8 . |
||||
Проведено обобщение записи уравнений состояния на нелинейные многомерные динамические объекты и системы управления, имеющие протяжение в пространстве и элементы транспортного запаздывания. Обобщение осуществлено путем включения звеньев запаздывания, наряду с интеграторами, в состав простейших динамических, т.е. таких, выходные величины которых трактуются как самостоятельные переменные состояния.
1. Инерционные динамические объекты
Традиционное математическое описание динамического объекта в переменных состояния включает векторное уравнение состояния, связывающее скорости изменения переменных состояния с воздействиями на объект и значениями самих переменных состояния, а также векторное уравнение, связывающее значения выходных величин объекта (или результатов их измерений) с его переменными состояния и воздействиями на него :
- x - вектор переменных состояния;
- u - вектор воздействий на объект;
- y - вектор выходных величин объекта;
- z - вектор помех;
- f(.) и g(.) - некоторые, довольно общего вида функции.
Система (К.1.1) - это система векторных дифференциально-алгебраических уравнений переменных состояния многомерного нестационарного сосредоточенного в пространстве (точечного) нелинейного инерционно-динамического объекта управления.
Из уравнений (К.1.1) нетрудно видеть, что описание динамического объекта без запаздываний структурно содержит всего три типа операторов: линейный дифференцирующий (собственно динамический, инерционный) и два безинерционных нелинейных: элемент связи и элемент композиции:
Линейный дифференцирующий оператор описывает инерцию потому, что задает мгновенную скорость изменения переменной состояния, а, следовательно, определяет значение известной на текущий момент переменной на некоторый, пусть небольшой интервал времени вперед. Это и следует трактовать как инерцию, т.е. некоторую предопределенность поведения.

Рис. К.1.1. Описание инерционного объекта и его структурная модель. Дифференциальное уравнение, отражает причинно-следственную связь воздействия х и реакции (отклика) y простейшего инерционного звена: воздействие х приводит к изменению выходной величины y такому, что скорость этого изменения прямо пропорциональна воздействию . Интегратор - модель простейшего, фундаментального динамического (инерционного) элемента. Структурная модель отображает то, как причина, воздействие, преобразуется в следствие, выходную величину: модель простейшей (фундаментальной) инерционности обеспечивает накопление и сохранение воздействия
В линеаризованной модели объекта справедлив принцип суперпозиции и поэтому оператор композиции переменных представляет собой их взвешенную сумму, а оператор связи становится линейным:
Уравнения динамического объекта в переменных состояния можно представить и в интегральном виде, более наглядном для структурного моделирования:

Уравнение состояния описывает собственную, внутреннюю инерционность динамического объекта. Уравнение выхода учитывает помехи измерению компонент вектора выходных величин.
Состояние и тенденция поведения хотя бы на бесконечно малый интервал вперед чисто инерционного динамического объекта определяется набором значений всех переменных состояния объекта в некоторый момент времени и отображается соответствующим положением изображающей точки в многомерном пространстве состояний. Поскольку эта информация для инерционного объекта без запаздывания исчерпывающая, то координаты любой точки траектории изображающей точки могут рассматриваться как начальные условия для интегрирования уравнений состояния, т.е. для определения всей последующей траектории движения изображающей точки, оценке поведения динамического объекта под внешними воздействиями или в отсутствие таковых.
В качестве иллюстрации этого приведем фазовые портреты (траектории движения изображающих точек объектов в двумерном пространстве состояний) для модели свободной колебательной системы с отличающимися начальными условиями:

Рис. К.1.1. Фазовые портреты свободной инерционной колебательной системы при разных начальных условиях, соответствующих одной и той же фазовой траектории совпадают, т.е. координаты любой точки фазовой траектории могут рассматриваться как начальные условия, полностью определяющие дальнейшее свободное поведение объекта
Таким образом, поведение точечных (исключительно инерционных, не имеющих элементов запаздывания) динамических объектов полностью описывается уравнениями состояния и выхода, а также начальными условиями, представляющими собой значения всех переменных состояния объекта в некоторый момент времени, и отображается некоторой траекторией, а текущее состояние объекта характеризуется точкой в многомерном пространстве переменных состояния.
2. Уравнения состояния протяженных объектов с элементами запаздывания
Учет звеньев запаздывания в моделях объектов как второго, самостоятельного вида простейших динамических элементов, наряду с инерционными (интеграторами), позволяет единообразно описывать в переменных состояния динамические объекты практически любой сложности и на этой основе проводить их анализ и оптимизацию.
2.1. Уравнения и структура моделей протяженных динамических объектов
Дифференциальная форма уравнений состояния протяженного объекта
Наличие элементов задержки в некоторых ветвях модели динамического объекта существенно, а часто и принципиально, изменяет динамические свойства объекта по сравнению с объектом без элементов запаздывания. Поэтому пространство состояний соответствующих только выходным величинам инерционных элементов (интеграторов) не в полной мере задает состояние и поведение объекта, имеющего звенья запаздывания.
Элемент запаздывания динамического объекта, также, как и инерционный, следует рассматривать как динамический, а его выходную величину - как отдельную переменную состояния.
Основание для отнесения звена задерживающего сигнал на конечный интервал времени к элементарным динамическим опирается на сходство и различия двух видов простейших динамических элементов моделей реальных объектов и состоит в следующем.
Внешнее отличие состоит в том, что инерционный элемент описывается элементарным дифференциальным уравнением, в то время как запаздывающий - алгебраическим.
Термин «динамический» относят к объектам, поведение которых под внешним воздействием можно предсказать хотя бы на бесконечно малый интервал. Инерционный элемент, интегратор, традиционно считающийся единственным динамическим, такому требованию отвечает. Но этому же требованию отвечает и звено запаздывания, если известна предыстория воздействия на него. В таком случает звено запаздывания позволяет жестко определить поведение его выходной величины на конечный интервал времени вперед. Т.о. звено запаздывания может быть отнесено к динамическим.
С другой стороны, звено запаздывания соответствует в реальных объектах либо переносу материалов («транспортное запаздывание»), либо задержке поступления сигнала (модели воздействия) на вход некоторого элемента объекта, связанной с распространением его в пространстве. Таким образом, звено запаздывания может быть отнесено и к элементам связи.
Нестационарный элемент запаздывания, обладающий дисперсией, и его частный случай, элемент чистой задержки, также как и простейший инерционный элемент является динамическим потому, что его выходной сигнал своеобразен, не может быть получен безинерционной композицией других, только инерционных переменных состояния. Это результат задержки по времени такой композиции.
Для обобщения уравнений состояния точечных объектов, представленных в форме Коши, на протяженные объекты и объекты с транспортным запаздыванием формально введем оператор прогнозирования Fwd{τ} :
Этот оператор в общем случае, естественно, физически не реализуем, поскольку должен абсолютно точно предсказывать значение переменной, на которую он воздействует, на конечный интервал τ времени вперед. Но этот оператор нужен всего лишь для формального «красивого» исходного представления уравнений состояния, а их структурное решение возможно с использованием реализуемого оператора запаздывания. С другой стороны, оператор прогнозирования в уравнениях состояния действует только на переменную состояния такую, значения которой определяются предысторией поведения всех переменных состояния объекта с запаздыванием и входных воздействий, т.е. некоторой композиции таковых, и поэтому, в этом частном случае, он реализуем, поскольку прогноз жестко определяется предысторией.
Итак, запишем векторные уравнения переменных состояния протяженного динамического объекта в виде:

В (К.2.1.2) для удобства записи и чтения переменные состояния разделены на две группы. Переменные x (1) первой группы это переменные состояния простейших инерционных элементов объекта, их выходные величины. Переменные x (2) это переменные состояния, соответствующие выходам звеньев запаздывания объекта. Очевидно, что в принципе, «инерционные» и «запаздывающие» переменные состояния могут быть записаны и пронумерованы и в произвольном порядке и объединены в одном векторном уравнении.
Отметим, что обобщенная система уравнений состояния динамического объекта имеет только одну независимую переменную - время t. Пространственные же характеристики объекта в (К.2.1.2) описываются косвенно, путем учета вектора времен задержек τ, обусловленных распространением воздействий в пространстве с конечной (не бесконечной) скоростью или транспортным запаздыванием.
Рассмотрение динамических объектов с запаздыванием на основе описания их уравнениями состояния проводилось некоторыми авторами и ранее .
В п. 2.1, (2.1.2), описание ограничивается указанием на задержки только в правых частях уравнений и не включает звенья запаздывания в структуру модели в качестве функционирующих элементов, определяемых собственными переменными состояния. Похожее исходное представление уравнений состояния используется и в , «1.5. Оптимальное управление системами с транспортным запаздыванием», стр.188 и далее, а также в .
Форма уравнений (К.2.1.2) отличается от предложенной в введением специальных переменных состояния, соответствующих выходным величинам звеньев запаздывания. Этим самым звенья запаздывания отнесены с простейшим динамическим и описание динамических объектов становится универсальным.
В предлагаемом в настоящей статье представлении динамического объекта текущее внутреннее состояние объекта полностью определяется вектором значений переменных состояния, соответствующих выходным величинам интеграторов и звеньев запаздывания, и предысторией их поведения.
Интегральная форма уравнений состояния протяженного объекта
Уравнения переменных состояния динамического объекта с запаздыванием могут быть представлены в интегрально-«запаздывающей» форме, которая, пожалуй, является более наглядной для составления структурной модели объекта:

где операторы задержки:
осуществляют обратное по действию по отношению к оператору прогноза Fwd{.} .
Итак, (К.2.1.3) - интегрально-«запаздывающие» уравнения векторных переменных состояния многомерного протяженного нелинейного нестационарного динамического объекта. Часть переменных, соответствующая выходным сигналам простейших инерционных элементов и обозначенная вектором x (1) , есть результат накопления (интегрирования) некоторой комбинации всех переменных, которая, как и сами переменные, а также входные воздействия, может изменяться с течением времени. Вторая часть переменных состояния, обозначенная x (2) , представляет собой задержку некоторой комбинации всех переменных состояния, а также и входных воздействий объекта, на некоторое время τ (вектор), которое может в общем случае меняться с течением времени. В соответствии с этими уравнениями могут быть построены структурные, в т.ч. виртуально-аналоговые, модели динамических объектов .
Начальные условия уравнений состояния протяженного объекта
В уравнениях (К.2.1.3) начальные условия для звеньев (операторов) задержки это не просто значения комбинаций переменных состояния и входных воздействий в нулевой момент времени, как это имеет место для интеграторов. Для однозначного решения уравнений (К.2.1.3) требуется задать начальные условия для звеньев запаздывания в виде функций, определяющих историю поведения входных величин этих звеньев на тот интервал времени назад, на который они осуществляют задержку.
Т.о. звенья запаздывания, обладая «памятью», требуют больше информации для однозначного решения вопроса о поведении объекта: не просто вектор значений переменных состояния в некоторый, условно нулевой момент времени, как этого достаточно для интеграторов, но вектор функций (комбинаций переменных состояния и входных воздействий на объект), заданных на соответствующих звеньям запаздывания временных интервалах, предшествующих началу интегрирования.
Другими словами, состояние и поведение динамического объекта, как точки и траектории в пространстве состояний для систем с запаздыванием определяется не только положением точки в этом пространстве, но и ее предыдущей траекторий как в подпространстве «запаздываний» x(2), так и в подпространстве x(1) «инерционных» переменных, а также историей поведения внешних воздействий в течение тех интервалов времени, на которые происходит задержка в соответствующих звеньях запаздывания.
Аналогичное утверждение для традиционной формы представления уравнений состояния объектов с запаздыванием приводится и в п. 2.1:
«Состояние непрерывного объекта с запаздыванием в произвольный момент времени характеризуется не только некоторым конечным числом параметров (имеются в виду переменные состояния - Ф.Б.Т.) (как в случае объектов без запаздывания), но и некоторыми функциями, определенными соответственно на интервале , . Это значительно усложняет решение задач управления такими объектами».
Вообще говоря, проблема задания начальных условий для звеньев запаздывания свойственна не только описанию динамического объекта в переменных состояния, но и для других методов описания. Часто при цифровом моделировании динамических объектов с запаздыванием принимают начальную траекторию «запаздывающих» переменных, т.е. выходных величин звеньев запаздывания постоянной. Для этого буфер звена заполняется в исходном состоянии нулями или константой.
Входной сигнал звена запаздывания, входящего в состав динамического объекта, представляет собой композицию переменных состояния, относящихся к другим звеньям, и воздействий на объект, поэтому задание жесткого прогноза изменения выходного сигнала звена запаздывания эквивалентно заданию предыстории поведения названных переменных состояния и воздействий на тот же интервал времени.

Рис. 2.1.1. Состояние динамического объекта с запаздыванием в некоторый момент времени характеризуется положением его изображающей точки в пространстве состояний, координатами которой являются значения переменных состояния в этот момент времени, а также траекторией этой точки в предшествующие текущему моменты времени. Многомерное пространство состояния можно представить в виде совокупности подпространства инерционных переменных состояния и подпространства «задержанных» переменных состояния
Таким образом, для точечных объектов положение изображающей точки в пространстве состояний в некоторый момент времени полностью определяет состояние динамического объекта и тенденцию его поведения в ближайшее время. Для объектов, протяженных в пространстве, имеющих в своей структуре звенья транспортного запаздывания, их состояние и последующее поведение определяется не только текущим положением изображающей точки, но и траекторией ее движения в пространстве состояний в предшествующий, может быть достаточно большой, интервал времени.
Структура модели динамического объекта с запаздываниями
Структура модели динамического объекта с запаздываниями, соответствующая системе (К.2.1.3) в укрупненном виде представлена на рисунке:

Рис. К.2.1.2. Укрупненное схематическое изображение основных структурных элементов модели наблюдаемого многомерного нестационарного протяженного в пространстве нелинейного динамического объекта управления. Собственные динамические свойства объекта определяются структурой, характеристиками и параметрами левого блока, блок преобразователя осуществляет преобразование переменных состояния в величины, которые могут быть измерены (или непосредственно в результаты измерений)

Рис. K.2.1.3. Структура модели собственно динамического объекта, отражающая его внутренний «метаболизм», т.е. направления передачи значений воздействий и переменных, а также операции, осуществляемые над ними. Поведение объекта с запаздыванием определяется не только вектором начальных условий «инерционных» переменных состояния, но и предысторией всех переменных состояния, а также и предысторией воздействий на объект
Сложный динамический объект с функциональными элементами запаздывания структурно представляется двумя параллельными контурами, инерционным и «запаздывающим». Переменные состояния всего объекта это объединение инерционных и «запаздывающих» переменных состояния (выходных величин простейших инерционных элементов в структуре объекта, и «запаздывающих», т.е. выходных величин звеньев запаздывания) в один вектор.
Как отмечалось выше, в общем случае, входной сигнал некоторого звена запаздывания определяется как всеми переменными состояния объекта, так и всеми воздействиями на него. Поэтому, для того, чтобы однозначно определить состояние, а затем и поведение объекта, необходимо знать значения и прогноз поведения «запаздывающих» переменных состояния, или, что эквивалентно, предысторию поведения всех переменных состояния и входных воздействий объекта.
2.2. Простейшие структурные элементы протяженных объектов
Как видно из уравнений (K.2.1.2) и (K.2.1.3) состояния и выхода динамических объектов с запаздыванием, для их описания достаточно всего четырех операторов. Математическое описание всех четырех простейших элементов (виртуальных аналогов этих операторов) динамических систем и объектов, имеющих пространственное протяжение и (или транспортное запаздывание), опосредованно опирающихся на физические законы их описывающие, сводится к простым уравнениям, одно из которых линейное дифференциальное, а три остальные - алгебраические:
- х - воздействие на элемент,
- y - его реакция,
- t - время,
- τ - некоторая задержка во времени.

Рис. K.2.2.1. Интегратор и стационарное звено запаздывания - исчерпывающий набор видов элементарных динамических объектов. Эти простейшие динамические элементы моделей объектов с запаздыванием требуют для полного и однозначного описания состояния и поведения объекта задания начальных условий. Для интегратора это просто значение выходной величины в условный нулевой момент времени, для звена запаздывания «начальное» условие это поведение входной величины в предшествующие моменты времени на интервале [-τ, 0], или, что то же самое, прогноз поведения выходной величины звена запаздывания («запаздывающей» переменной состояния) на интервал , равный времени задержки в звене

Рис. K.2.2.2. Простейшие (фундаментальные) элементы общего вида структурной схемы динамического объекта как его математической модели насчитывают только четыре разного типа элементов. Элементов этих типов достаточно для моделирования сколь угодно сложного динамического объекта (технологической установки, системы управления ей и т.п.)
Комбинируя простейшие элементы можно построить состоятельную модель сколь угодно сложного динамического объекта. Составление системы дифференциально-алгебраических уравнений динамического объекта в виде уравнений состояния это неявный, опосредованный способ, некое «таинство», представления модели динамического объекта в виде набора взаимодействующих между собой однонаправленных простейших динамических элементов.
2.3. Наблюдаемость и управляемость объектов с запаздыванием
Из проведенного выше рассмотрения следует, что однозначное состояние динамического объекта с запаздыванием определяется не только текущими значениями переменных состояния, но и историей их изменения в предыдущие моменты времени, на конечном и достаточно протяженном интервале. Поэтому для таких объектов следует уточнить понятия наблюдаемости и управляемости.
Управляемость динамического объекта с элементами запаздывания состоит в том, чтобы имелась возможность за конечное время конечным изменением вектора воздействий перевести объект из текущего состояния, которому предшествовало некоторое определенное поведение, в новое, требуемое состояние, которому предшествует заданная траектория изображающей точки в пространстве состояний.
Наблюдаемость объекта с запаздыванием определим как возможность нахождения текущего вектора переменных состояния в любой момент времени и конечный участок траектории в пространстве состояний, по которой изображающая точка попадает в текущее положение, по измерениям выходных величин объекта и их поведения в течение некоторого предшествующего интервала времени.
Более строгие определения понятий наблюдаемости и управляемости динамических объектов в представлении запаздываний в правых частях уравнений состояния можно посмотреть в : «2.6. Управляемость и наблюдаемость систем с запаздыванием».
2.4. Состояние и начальные условия динамического объекта с запаздыванием
Текущее состояние динамического объекта с запаздыванием должно однозначно определять его поведение в последующие моменты времени, хотя бы на весьма короткий интервал. В отсутствие внешних воздействий на объект (свободное движение), или при известных внешних воздействиях, это время простирается до бесконечности.
Состояние динамического объекта с запаздыванием определяется мгновенным значением всех переменных состояния, «инерционных» и «запаздывающих», а также их предысторией и предысторией воздействий на объект.

Рис. К.2.4.1. Фазовые портреты и поведение переменных состояния динамического объекта с запаздыванием в отсутствие внешних воздействий. Если рассматривать звено с запаздыванием как элементарное динамическое, т.е. считать его выходную величину как самостоятельную переменную состояния, то для полного описания состояния и тенденции поведения динамического объекта с запаздыванием требуется задать не только значения переменных состояния в некоторый момент времени, но и предысторию их изменения, помещенную в данном случае в буфер звена запаздывания. Разные предыстории приводят к разным траекториям фазового портрета, т.е. к разному поведению объекта. Прогноз поведения выходной переменной звена запаздывания (переменной состояния х3) эквивалентен предыстории поведения его входной величины, поскольку представляет собой задержанную на время запаздывания, в данном случае τ = 1 сек, эту самую предысторию. Интервал, на котором следует знать предысторию определяется величиной задержки в звене запаздывания
Как видно, для задания начальных условий уравнений состояний, а также, что эквивалентно, для однозначного описания текущего состояния динамического объекта с запаздыванием необходимо знать не только значения переменных состояния, но и их предысторию.

Рис. K.2.4.2. Начальные условия, или что эквивалентно, состояние инерционно-динамических объектов и инерционно-динамических объектов с запаздыванием. Для чисто инерционного объекта для всестороннего описания его свойств достаточно знать значения всех переменных состояния в некоторый момент времени, а также, значения входных воздействий на объект, если таковые существуют. Объект с запаздываниями требует не только знания значений всех переменных состояния, как инерционных (выходных сигналов интеграторов модели), так и «запаздывающих» (выходных сигналов звеньев запаздывания модели), но и иметь прогноз поведения «запаздывающих»
Таким образом, для описания объектов с запаздыванием требуется значительно больше информации, чем для просто инерционных объектов, что усложняет их анализ и оптимизацию.
2.5. О полном пространстве состояний цифровой модели динамического объекта с запаздыванием и его состоятельном подпространстве
Модели реальных непрерывных инерционных динамических объектов без запаздывания могут быть построены как с использованием исключительно интеграторов (W(p) - модель), так и с использованием только элементарных звеньев запаздывания (W(z)-модель):
Рис. 2.5.1. (анимация, 14 кадров) Модели инерционной колебательной системы, построенные на базе интеграторов и на базе элементарных звеньев запаздывания, осуществляющих задержку на один такт, эквивалентны, как это видно по переходным функциям выходных величин, х1 и z1 соответственно. Естественно, переменные состояния этих моделей, соответствующие выходным величинам интеграторов и звеньев задержки сигналов на такт моделирования разные. Поэтому и траектории изображающих точек разных пар переменных - разные. Конечно, у модели на элементарных звеньях запаздывания траектория изображающей точки довольно «скучная», идет по диагонали, поскольку обе переменные отличаются на незначительную величину, что принципиально важно для обеспечения состоятельности модели
Отметим, что интеграторами (апериодическими звеньями) нельзя даже приближенно промоделировать звенья с достаточно большим запаздыванием, в то время как любое запаздывание без проблем с любой точностью моделируется звеньями задержки на такт, достаточно только выбрать их достаточное число.

Рис. 2.5.2. Непрерывное звено запаздывания и его цифровые модели. Переменная состояния, несущая содержательную, исчерпывающую информацию это выходная величина звена запаздывания с учетом предыстории поведения его входного воздействия. Выходные сигналы промежуточных элементов дискретной модели звена запаздывания формально можно отнести к переменным состояния, однако, поскольку информация в них повторяется со сдвигом, достаточно ограничиться только выходной величиной всего звена и рассматривать его как элементарное унитарное динамическое, состояние которого определяется не только значением выходной величины, но и ее прогнозом (предысторией входной величины). Буфер унитарной дискретной модели заполнен предысторией входной величины, поэтому прогноз переменной состояния жестко определяется этой предысторией
Определение переменной состояния, отнесенной к звену запаздывания, собственно, равной последней величине микрозвеньев буфера запаздывания, позволяет использовать в качестве состоятельного подпространства состояний такое, которое включает только выходные величины элементарных звеньев, составляющих цифровую модель звена запаздывания. Относительно малое число эффективных переменных состояния особенно важно при аналитическом исследовании динамического объекта и графическом представлении его результатов.
Заключение
Звено запаздывания на конечную величину может рассматриваться в дополнение к интегратору как простейший динамический элемент, выходная величина которого является самостоятельной переменной состояния, причем для полного и однозначного описания состояния объекта необходимо знать как положение изображающей точки в пространстве состояний, так и часть ее предыдущей траектории, т.е предысторию поведения объекта.
Оптимальная система управления, если она уже реализована, существует объективно и ее характеристики не зависят от того, каким математическим аппаратом она была описана и с помощью каких математических методов и инструментов она была оптимизирована. Поэтому простота математического описания системы управления, в частности САР, должна определяться сложностью системы, ей соответствовать.
Литература и Интернет
- 1. Ким Д.П. Теория автоматического управления. Т.2. Многомерные, нелинейные, оптимальные и адаптивные системы: Учеб. Пособие. - М.: ФИЗМАТЛИТ, 2004. - 464 с. - ISBN 5-9221-0534-5.
- 2. Ким Д.П. Сборник задач по теории автоматического управления. Многомерные, нелинейные, оптимальные и адаптивные системы. - М.: ФИЗМАТЛИТ, 2008. - 328 с. - ISBN 978-5-9221-0937-6.
- 3. Yuan Yan. Automatic Control Theory. Chapter 1-9. Presentation, pdf-format. School of
Information Science and Engineering, CSU. 28.8.2005
http://wuhua.csu.edu.cn/ac/ac/ch1.pdf
http://wuhua.csu.edu.cn/ac/ac/ch2.pdf
...
http://wuhua.csu.edu.cn/ac/ac/ch9.pdf - 4. Лукас В.А. Теория управления техническими системами. Компактный учебный курс для вузов. - 3-е издание, перераб. и дополн. - Екатеринбург. Изд-во УГГА, 2002, - 675 с.
- 5. Д. Сю, А. Мейер. Современная теория автоматического управления и ее применение. Перевод с английского В. С. БОЧКОВА, Е. В. ГУРЕЦКОЙ, Л. М. КИСЕЛЕВОЙ и В. Г. ПОТЕМКИНА. Под редакцией д.т.н. профессора Ю. И. ТОПЧЕЕВА. -М., : МАШИНОСТРОЕНИЕ, 1972.
- 6. Дорф Р., Бишоп Р. Современные системы управления. Пер. с англ. Копылова Б.И. - М. :Лаборатория базовых знаний, С_Пб, 2002. -832 с. ISBN 5-93208-119-8
- 7. Федосов Б.Т. Многомерные объекты. Описание, анализ и управление. Рудный, 2010.
http://model.exponenta.ru/bt/bt_171_MultyDim_Obj_Contr.htm - 8. Ю.Ю. Громов и др. Системы автоматического управления с запаздыванием. -Тамбов. :Издательство
ТГТУ, 2007.
http://window.edu.ru/window_catalog/files/r56879/k_Gromov1.pdf (698 КБ) - 9. Калман Рудольф Э., Фалб Питер Л., Арбиб Майкл А. Очерки по математической теории систем: Пер. с англ.
/ Под ред. Я.3.Цыпкина. Предисл. Э.Л.Наппельбаума. Изд. 2-е, стереотипное. — М.: Едиториал
УРСС, 2004. - 400 с. ISBN 5-354-00762-3
R.E.Kalman, R.L.Falb, M.A.Arbib
Topics in mathematical system theory - 10. Ф. Чаки. Современная теория управления. Нелинейные, оптимальные и адаптивные системы. Перевод с английского В. В. Капитоненко и С. А. Анисимова. Под редакцией Н. С. Райбмана М., : МИР 1975
- 11. В.М. Синеглазов, Р.Ю. Ткачев. Автономное управление многомерным объектом с запаздываниями общего вида. Кибернетика и вычисл. техника. Межведомственный сборник научных трудов. Вып. 157. Киев, 2009, с. 17 -25.
Благодарности
Системы с запаздыванием отличаются от рассмотренных ранее систем тем, что в одном или нескольких из своих звеньев имеют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величину т, называемую временем запаздывания, причем это время запаздывания остается постоянным и во всем последующем ходе процесса.
Например, если звено описывается уравнением
(апериодическое звено первого порядка), то уравнение соответствующего звена с запаздыванием будет иметь вид
(апериодическое звено первого порядка с запаздыванием). Такого вида уравнения называются уравнениями с запаздывающим аргументом,
![]() Тогда уравнение (6.31) запишется в обыкновенном
Тогда уравнение (6.31) запишется в обыкновенном
изменяется скачком от нуля до единицы (рис. 6.20,
![]() стоящей в правой части уравнении звена,
стоящей в правой части уравнении звена,

). В общем случае, как и для (6.31), уравнение динамики любого звена с запаздыванием можно разбить на два:

что соответствует условной разбивке звена с запаздыванием (рис. 6.21, а) па два: обыкновенное звено того же порядка и с теми же коэффициентами и предшествующий ему элемент запаздывания (рис. 6.21,6).

означает время движения металла от валков до измерителя толщины. В двух последних примерах величина т называется транспортным запаздыванием.
В первом приближении определенной величиной запаздывания т могут быть охарактеризованы трубопроводы или длинные электрические линии, входящие в звенья системы.
показанная на рис. 6.22, б, то можно приближенно описать это звено как апериодическое звено первого порядка с запаздыванием (6.31), взяв величины т, Г и к с экспериментальной кривой (рис, 6,22, б).
Заметим также, что такая же экспериментальная кривая согласно графику рис. 6.22, в может трактоваться и как временная характеристика обыкновенного апериодического звена второго порядка с уравнением
и к можно вычислить из соотношений, записанных в § 4.5 для данного звена, по некоторым замерам на экспериментальной кривой или другими способами.
функция (6.36) мало отличается от передаточной функции звена с запаздыванием (6.35).
Уравнение любого линейного звена с запаздыванием (6.33) будем теперь записывать в виде
Передаточная функция линейного звена с запаздыванием будет
обозначена передаточная функция соответствующего обыкновенного звена без запаздывания.
![]() - модуль и фаза частотной передаточной функции звена без запаздывания.
- модуль и фаза частотной передаточной функции звена без запаздывания.

Отсюда получаем следующее правило.
Для построения амплитудно-фазовой характеристики любого звена с запаздыванием нужно взять характеристику соответствующего обыкновенного звена и каждую ее точку сдвинуть вдоль окружности по часовой стрелке на угол то, где со - значение частоты колебаний в данной точке характеристики (рис. 6.23, а).
начальная точка остается без изменения, а конец характеристики асимптотически навивается на начало координат (если степень операторного многочлена В меньше, чем многочлена С).
Выше говорилось о том, что реальные переходные процессы (временные характеристики) вида рис. 6.22, б часто могут быть с одинаковой степенью приближения описаны как уравнением (6.31), так и (6.34). Амплитудно-фазовые характеристики для уравнений (6.31) и (6.34) показаны на рис. 6.23, а и б соответственно. Принципиальное отличие первой состоит в том, что она имеет точку D пересечения с осью (/. При сравнении обеих характеристик между собой и с экспериментальной амплитудно-фазовой характеристикой реального звена надо принимать во внимание не только форму кривой, но и характер распределения отметок частот со вдоль нее.
Передаточная функция разомкнутой системы без запаздывания.
Характеристическое уравнение замкнутой системы, как показано в гл. 5, имеет вид
уравнение может иметь бесконечное количество корней.
Существенно изменяется очертание амплитудно-фазовой характеристики разомкнутой цени, построенной но частотной передаточной функции
причем размыкание системы производится по определенному правилу, которое дается ниже.
Как следствие, для устойчивости линейных систем первого и второго порядка с запаздыванием, оказывается, уже недостаточно только положительности.коэффициентов, а для систем третьего и более высокого порядка с запаздыванием неприменимы критерии устойчивости Вышнеградского, Рауса и Гурвица.
Ниже будет рассмотрено определение устойчивости только по критерию Найквиста, так как его использование для этой пели оказывается наиболее простым.
1Построение амплитудно-фазовой характеристики и исследование устойчивости но критерию Найквиста лучше всего производить, если передаточная функция разомкнутой системы представлена в виде (6.38). Для получения этого необходимо произвести соответствующим образом размыкание системы.
Для случая, изображенного на рис. 6.24, а, размыкание можно сделать в любом месте главной цепи, например так, как это показано. Тогда передаточная функция разомкнутой системы будет что совпадает по форме с (6.41).
Для случая, изображенного на рис. 6,24, б, размыкание главной цепи дает выражение

функции разомкнутой системы, не удобное для дальнейших исследований:


Наконец, в случае, изображенном на рис. 6.24, в, при размыкании системы в указанном месте получаем выражение, также совпадающее с (6.41):

Частотную передаточную функцию (6.41) можно представить в виде

Поэтому, представив выражение (6.41) в виде
Отступая на шаг, ты находишь себя, затем перемещаешься - и теряешь себя.
У. Эко. Маятник Фуко
Примеры математических моделей. Основные понятия
Предварительные терминологические замечания. В настоящей главе речь пойдет о моделях, основанных на использовании так называемых запаздывающих дифференциальных уравнений. Это частный случай уравнений с отклоняющимися коэффициентами 1 . Синонимы для этого класса - функционально-дифференциальные уравнения или дифференциальноразностные уравнения. Однако мы предпочтем пользоваться термином «запаздывающее уравнение» или «уравнение с запаздыванием».
Термин «дифференциально-разностные уравнения» нам еще встретится в другом контексте при анализе численных методов для решения уравнений в частных производных и к содержанию данной главы отношения не имеет.
Пример экологической модели с запаздыванием. В книге В. Воль- терры приведен следующий класс наследственных моделей, учитывающих не только текущую численность популяций хищника и жертвы, по и предысторию развития популяции:
Общая теория уравнений с отклоняющимся аргументом изложена в работах: Беллман Р., Кук К. Дифференциально-разностные уравнения. М. : Мир, 1967; Мышкис А. Д. Линейные дифференциальные уравнения с запаздывающим аргументом. М. : Наука, 1972; Хейл Дж. Теория функционально-дифференциальных уравнений. М.: Мир, 1984; ЭлъсгольцЛ. Э., Норкин С. Б. Введение в теорию дифференциальных уравнений с отклоняющимся аргументом. М.; Наука, 1971.
Система (7.1) относится к классу интегрально-дифференциальных моделей типа Вольтерры, К { , К 2 - некоторые интегральные ядра.
Кроме того, в литературе встречаются другие модификации системы «хищник - жертва»:
Формально в системе (7.2) нет интегральных членов, в отличие от системы (7.1), но прирост биомассы хищника зависит от численности видов не в данный момент, а в момент времени t - Т (под Т часто понимается время жизни одного поколения хищника, возраст половой зрелости самок хищника и т.п. в зависимости от содержательного смысла моделей). О моделях типа «хищник - жертва» см. также параграф 7.5.
Казалось бы, что системы (7.1) и (7.2) имеют существенно разные свойства. Однако при специальном виде ядер в системе (7.1), а именно 8-функции /?,(0 - t) = 8(0 - 7^), К 2 (д - t) = 8(0 - Т 2) (о 8-функции приходится говорить несколько условно, так как обобщенные функции определяются как линейные функционалы, а приведенная система нелинейная), система (7.1) переходит в систему
Очевидно, что система (7.3) устроена следующим образом: изменение численности популяции зависит не только от текущей численности, но и от численности предыдущего поколения. С другой стороны, система (7.3) есть частный случай интегрально-дифференциального уравнения (7.1).
Линейное уравнение с запаздыванием (запаздывающего типа). Линейным дифференциальным уравнением запаздывающего типа с постоянными коэффициентами будем называть уравнение вида
где а, Ь,Т - постоянные; Т> 0;/- заданная (непрерывная) функция на К. Без ограничения общности в системе (7.4) можно положить Т= 1.
Очевидно, если задана функция x(t) y t е [-Г; 0], то возможно определить x(t) при t е и являющаяся решением уравнения (7.4) для t> 0. Если ф(?) имеет производную в точке t = 0, причем ф(0) = ато производная 4"(ф|,_ 0 является двусторонней.
Доказательство. Определим функцию x(t) = ф(?) на |-7"; 0]. Тогда решение (7.4) можно записать на в виде
(применена формула вариации постоянных). Поскольку функция x(t ) известна на . Этот процесс можно продолжать неограниченно. Обратно, если функция х(?) удовлетворяет формуле (7.5) на ). Выясним вопрос об устойчивости данного решения. Подставляя в уравнение (7.8) малые отклонения от единичного решения z(t) = 1 - y(t), получим
Данное уравнение исследовано в литературе , где показано, что оно удовлетворяет ряду теорем о существовании периодических решений. При а = тт/2 происходит бифуркация Хопфа - из неподвижной точки рождается предельный цикл. Данный вывод делается из результатов анализа линейной части уравнения (7.9). Характеристическое уравнение для линеаризованного уравнения Хатчинсона имеет вид
Отметим, что изучение на устойчивость линеаризованного уравнения (7.8) есть исследование устойчивости стационарного состояния y(t) = 0. При этом получается А, = а > 0, стационарное состояние неустойчиво и бифуркации Хопфа не происходит.
Далее Дж. Хейл показывает, что уравнение (7.9) имеет ненулевое периодическое решение для каждого а > л/2. Кроме того, там без доказательства приведена теорема о существовании периодического решения (7.9) с любым периодом р > 4.
Линейными системами с запаздыванием называются такие автоматические системы, которые, имея в общем ту же самую структуру, что и обыкновенные линейные системы (раздел II), отличаются от последних тем, что в одном или нескольких из своих звеньев имеют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величину называемую временем запаздывания, причем это время запаздывания остается постоянным и во всем последующем ходе процесса.
Например, если обыкновенное линейное звено описывается уравнением
![]()
(апериодическое звено первого порядка), то уравнение соответствующего линейного звена с запаздыванием будет иметь вид
(апериодическое звено первого порядка с запаздыванием). Такого вида уравнения называются уравнениями с запаздывающим аргументом или дифференциально-разностными уравнениями.

Обозначим Тогда уравнение (14.2) запишется в обыкновенном виде:
![]()
Так, если входная величина изменяется скачком от нуля до единицы (рис. 14.1, а), то изменение величины стоящей в правой части уравнения звена, изобразится графиком рис. 14.1, б (скачок на секунд позже). Используя теперь переходную характеристику обыкновенного апериодического звена в применении к уравнению (14.3), получаем изменение выходной величины в виде графика рис. 14.1, в. Это и будет переходная характеристика апериодического звена первого порядка с запаздыванием (его апериодическое «инерционное» свойство определяется постоянной времени Т, а запаздывание - величиной
Линейное звено с запаздыванием. В общем случае, как и для (14.2), уравнение динамики любого линейного звена с запаздыванием можно
разбить на два:

что соответствует условной разбивке линейного звена с запаздыванием (рис. 14.2, а) на два: обыкновенное линейное звено того же порядка и с теми же коэффициентами и предшествующий ему элемент запаздывания (рис. 14,2, б).
Временная характеристика любого звена с запаздыванием будет, следовательно, такая же, как у соответствующего обыкновенного звена, но только сдвинута по оси времени вправо на величину .
Примером звена «чистого» запаздывания является акустическая линия связи - время прохождения звука). Другими примерами могут служить система автоматического дозирования какого-либо вещества, перемещаемого с помощью ленточного транспортера - время движения ленты на определенном участке), а также система регулирования толщины прокатываемого металла, где означает время движения металла от валков до измеритетя толщины


В двух последних примерах величина называется транспортным запаздыванием.
В первом приблилчвнии определенной величиной запаздывания могут быть оларактеризованы трубопроводы или длинные электрические линии, входящие в звенья системы (подробнее о них см. § 14.2).
Величину запаздывания в звене можно определить экспериментально путем снятия временной характеристики. Например, если при подаче на вход звена скачком некоторой величины, принимаемой за единицу, на выходе получается экспериментальная кривая для показанная на рис. 14.3, б, то можно приближенно описать это звено как апериодическое звено первого порядка с запаздыванием (14.2), взяв величины с экспериментальной кривой (рис. 14.3, б).
Заметим также, что такая же экспериментальная кривая согласно графику рис. 14.3, в может трактоваться и как временная характеристика обыкновенного апериодического звена второго порядка с уравнением
причем и к можно вычислить из соотношений, записанных в § 4.5 для данного звена, по некоторым замерам на экспериментальной кривой или другими способами.
Итак, с гочки зрения временной характеристики реальное звено, приближенно описываемое уравнением первого порядка с запаздывающим аргументом (14.2), часто может быть с такой же степенью приближения описано обыкновенным дифференциальным уравнением второго порядка (14.5). Для решения вопроса о том, какое из этих уравнений лучше подходит к данному
реальному звену, можно сравнить еще их амплитудно-фазовые характеристики с экспериментально снятой амплитудно-фазовой характеристикой звена, выражающей его динамические свойства при вынужденных колебаниях. Построение амплитудно-фазовых характеристик звеньев с запаздыванием будет рассмотрено ниже.
В целях единства записи уравнений представим второе из соотношений (14.4) для элемента запаздывания в операторном виде. Разложив правую часть его в ряд Тейлора, получим
или, в принятой ранее символической операторной записи,
Это выражение совпадает с формулой теоремы запаздывания для изображений функций (табл. 7.2). Таким образом, для звена чистого запаздывания получаем передаточную функцию в виде
![]()
Заметим, что в некоторых случаях наличие большого числа малых постоянных времени в системе регулирования можно учесть в виде постоянного запаздывания, равного сумме этих постоянных времени. Действительно, пусть система содержит последовательно включенных апериодических звеньев первого порядка с коэффициентом передачи, равным единице, и величиной каждой постоянной времени Тогда результирующая передаточная функция будет
Если то в пределе получаем . Уже при передаточная функция (14.8) мало отличается от передаточной функции звена с запаздыванием (14.6).
Уравнение любого линейного звена с запаздыванием (14.4) будем теперь записывать в виде
Передаточная функция линейного звена с запаздыванием будет
где через обозначена передаточная функция соответствующего обыкновенного линейного звена без запаздывания.
Частотная передаточная функция получается из (14.10) подстановкой
где - модуль и фаза частотной передаточной функции звена без запаздывания. Отсюда получаем следующее правило.
Для построения амплитудно-фазовой характеристики любого линейного звена с запаздыванием нужно взять характеристику соответствующего обыкновенного линейного звена и каждую ее точку сдвинуть вдоль окружности по часовой стрелке на угол , где - значение частоты колебаний в данной точке характеристики (рис. 14.4, а).
Так как в начале амплитудно-фазовой характеристики а в конце то начальная точка остается без изменения, а конец характеристики асимптотически навивается на начало координат (если степень операторного многочлена меньше, чем многочлена
Выше говорилось о том, что реальные переходные процессы (временные характеристики) вида рис. 14.3, б часто могут быть с одинаковой степенью приближения описаны как уравнением (14.2), так и (14.5). Амплитудно-фазовые характеристики для уравнений (14.2) и (14.5) показаны на рис. 14.4, а и соответственно. Принципиальное отличие первой состоит в том, что она имеет точку D пересечения с осью

При сравнении обеих характеристик между собой и с экспериментальной амплитудно-фазовой характеристикой реального звена надо принимать во внимание не только форму кривой, на и характер распределения отметок частот о вдоль нее.
Линейная система с запаздыванием.
Пусть одноконтурная или многоконтурная автоматическая система в числе своих звеньев имеет одно звена с запаздыванием. Тогда уравнение этого звена имеет вид (14.9). Если таких звеньев несколько, то они могут иметь разные величины запаздывания Все выведенные в главе 5 общие формулы для уравнений и передаточных функций систем автоматического регулирования остаются в силе и для любых линейных систем с запаздыванием, если только в эти формулы подставлять значения передаточных функций в виде (14.10).
Например, для разомкнутой цепи из последовательно соединенных звеньев, среди которых имеется два звена с запаздыванием соответственно, передаточная функция разомкнутой системы будет иметь вид
где - передаточная функция разомкнутой цепи без учета запаздывания, равная произведению передаточных функций включенных последовательно звеньев.
Таким образом, при исследовании динамики разомкнутой цепи из последовательно соединенных звеньев безралично, будет ли все запаздывание сосредоточено в одном каком-нибудь звене или разнесено по разным звеньям. Для многоконтурных цепей получатся более сложные соотношения.
Если имеется звено с отрицательной обратной связью, обладающей запаздыванием , то оно будет описываться уравнениями;