Признаки сходимости числовых рядов. Высшая математика. Теория рядов Что называется частичной суммой ряда

Произведите предварительную проверку. Есть простая теорема, которая гласит, что если бесконечная сумма функции f сходится, то предел функции f равен 0. Таким образом, если мы имеем функцию x^2, то у нее нет предела, и ее сумма до бесконечности расходится; с другой стороны, предел функции 1/x равен 0, так что ее сумма может сходиться. Если предел не равен нулю, мы знаем, что ряд расходится. ВНИМАНИЕ: обратное не верно, то есть то, что предел равен нулю, совсем не означает, что ряд обязательно сходится. В этом случае необходима дальнейшая проверка.

Геометрические ряды. Для этих рядов существует очень простое правило, так что прежде всего определите, не является ли ваш ряд геометрическим. Геометрический ряд -- это последовательность чисел, каждый член которой можно представить в виде r^k, где k -- переменная, а r -- число, лежащее в интервале между -1 и 1. Геометрические ряды всегда сходятся. Более того, вы легко можете определить сумму такого ряда, которая равна 1/(1-r).

Обобщенные гармонические ряды, или ряды Дирихле. Таким рядом называется сумма функций вида 1/(x^p), где x -- любое число. Теорема для этих рядов гласит, что если p больше единицы, ряд сходится, если же p меньше или равно единице, ряд расходится. Это означает, что упомянутый выше ряд 1/x расходится, так как его можно представить в виде 1/(x^1), где p=1. Этот ряд называется гармоническим. Ряд 1/(X^2) сходится, поскольку 2 больше 1.

Другие ряды. Если ряд не принадлежит одному из типов, указанных выше, примените к нему методы, приведенные ниже. Если не помог один метод, примените следующий, поскольку не всегда ясно, какой из них следует выбрать. Хотя и не существует однозначных правил, со временем вы сможете лучше ориентироваться в выборе нужного метода.

• Метод сравнения. Допустим, у вас есть два ряда, состоящие из положительных членов, a(n) и b(n). Тогда: 1) если бесконечная сумма b(n) сходится, и a(n) меньше чем b(n) (для любого достаточно большого n), тогда сумма a(n) также сходится; 2) если b(n) расходится, и a(n)>b(n), тогда a(n) тоже расходится. Например, у вас есть ряд 2/x; мы можем сравнить его с рядом 1/x. Поскольку мы уже знаем, что ряд 1/x расходится, и 2/x > 1/x, отсюда следует, что ряд 2/x также расходится. Таким образом, идея метода состоит в том, чтобы определить, сходится или нет исследуемый ряд, используя уже известный ряд.
• Метод сравнения пределов. Если a(n) и b(n) являются рядами положительных чисел, и если существует предел a(n)/b(n), который больше 0, тогда оба ряда либо сходятся, либо расходятся. В этом случае исследуемый ряд также сравнивается с известным; метод состоит в том, чтобы подобрать известный ряд, максимальная степень которого соответствует степени исследуемого ряда. Например, если вы рассматриваете ряд 1/(x^3+2x+1), имеет смысл сравнить его с рядом 1/(x^3).
• Проверка интегралом. Если функция больше нуля, непрерывна и уменьшается при значениях x больше или равных 1, тогда бесконечный ряд f(n) сходится, если определенный интеграл от 1 до бесконечности от функции f(x) существует и имеет конечное значение; в противном случае ряд расходится. Таким образом, достаточно проинтегрировать функцию и найти предел при x, стремящемся к бесконечности: если предел конечен, ряд сходится, если же предел равен бесконечности, ряд расходится.
• Знакопеременные ряды. Если a(k)>a(k+1)>0 при достаточно больших k, и предел a(n) равен 0, тогда знакопеременный ряд (-1)^n a(n) сходится. Проще говоря, допустим, что ваш ряд является знакопеременным (то есть его члены попеременно положительны и отрицательны); в этом случае отбросьте знакопеременную часть функции и найдите предел того, что осталось -- если предел конечен, ряд сходится.
• Метод отношения. Если дан бесконечный ряд a(n), найдите следующий член ряда a(n+1). Затем вычислите отношение последующего члена к предыдущему a(n+1)/a(n), в случае необходимости взяв его абсолютное значение. Найдите предел этого отношения при n стремящемся к бесконечности; если этот предел существует и конечен, это означает следующее: 1) если предел меньше единицы, ряд сходится; 2) если предел больше единицы, ряд расходится; 3) если предел равен единице, данный способ недостаточен (ряд может как сходиться, так и расходиться).
• Это основные методы определения сходимости рядов, и они чрезвычайно полезны. Если ни один из них не помог, вполне вероятно, что задача не имеет решения, или же вы где-то допустили ошибку. Эти способы могут быть использованы и для других рядов, таких как степенные ряды, ряды Тейлора и т.д. Владение данными методами сложно переоценить, поскольку других простых способов определить сходимость ряда не существует.

Какова сумма всех натуральных чисел? Интуиция подсказывает, что ответ - бесконечность. В математическом анализе сумма натуральных чисел является простым примером расходящегося ряда. Тем не менее, математики и физики сочли полезным придать дробные, отрицательные и даже нулевые значения суммам таких рядов. Цель моей статьи - желание отодвинуть завесу тайны, окружающую результаты суммирования расходящихся рядов. В частности, я буду использовать функцию Sum (функция поиска частичных сумм, рядов и т. п. в Mathematica ), а так же другие функции в Wolfram Language для того, чтобы объяснить в каком смысле стоит рассматривать следующие утверждения:

Важность обозначений формул буквами A, B, C, и D вскоре станет вам понятна.

Начнем с того, что напомним понятие сходящегося ряда, используя следующую бесконечно убывающую геометрическую прогрессию.

Общий член ряда, начиная с n = 0 , определяется по формуле:

Теперь зададим сумму членов ряда от i = 0 до некоторого конечного значения i = n .

Эта конечная сумма называется частичной суммой ряда .

График значений таких частичных сумм показывает, что их значения приближаются к числу 2 с ростом n :

Применяя функцию Limit (поиск предела последовательности или функции в точке) найдем предел значения частичных сумм этого ряда при стремлении n к бесконечности, что подтвердит наши наблюдения.

Функция Sum даёт такой же результат, когда мы производим суммирование членов ряда в пределах от 0 до бесконечности.

Мы говорим, что данный ряд (сумма данной бесконечно убывающей геометрической прогрессии) сходится и что его сумма равна 2.

Вообще, бесконечный ряд сходится, если последовательность его частичных сумм стремится к некоторому значению при неограниченном увеличении номера частичной суммы. В этом случае, предельное значение частичных сумм называется суммой ряда.

Бесконечный ряд который не сходится называется расходящимся . По определению, сумма расходящегося ряда не может быть найдена с помощью рассмотренного выше метода частичных сумм. Тем не менее, математики разработали различные способы присваивания конечных числовых значений суммам этих рядов. Такая сумма называется регуляризованной суммой расходящегося ряда. Процесс вычисления регуляризованных сумм называется регуляризацией .

Теперь мы рассмотрим пример A из вступления.

“A” обозначает Абеля, знаменитого норвежского математика, который предложил одну из техник регуляризации расходящихся рядов. В ходе своей короткой жизни, он умер всего в 26 лет, Абель достиг впечатляющих результатов в решении одних из самых трудных математических задач. В частности, он показал, что решение алгебраического уравнения пятой степени не может быть найдено в радикалах, поставив тем самым точку в проблеме, которая оставалась нерешенной на протяжении 250 лет до него.

Для того чтобы применить метод Абеля, заметим, что общий член данного ряда имеет вид:

Это можно легко проверить, найдя несколько первых значений a [n ].

Как можно увидеть на графике ниже, частичные суммы ряда принимают значения, равные 1 или 0 в зависимости от того, четное n или нечетное.

Естественно, что функция Sum выдает сообщение, о том что ряд расходится.

Регуляризация Абеля может быть применена к этому ряду в два шага. Сначала мы строим соответствующий степенной ряд.

Затем мы берем предел этой суммы при x стремящемся к 1, заметим при этом, что соответствующий ряд сходится для значений x меньших, но не равных 1.

Эти два шага можно объединить, сформировав, по сути, определение суммы расходящегося ряда по Абелю .

Мы можем получить тот же ответ используя опцию Regularization для функции Sum следующим образом.

Значение 1 / 2 представляется разумным, так как оно является средней величиной из двух значений, 1 и 0, принимаемых частичной суммой данного ряда. Кроме того, используемый в данном методе предельный переход интуитивно понятен, т. к. при x = 1 степенной ряд совпадает с нашим расходящимся рядом. Однако, Абель был сильно обеспокоен отсутствием строгости, которое было присуще математическому анализу того времени, и выражал свою обеспокоенность об этом:

«Расходящиеся ряды - изобретение дьявола, и это стыдно на них ссылаться при каких бы то ни было доказательствах. С их помощью, можно сделать любой вывод, какой ему будет угоден, и именно поэтому эти ряды производят столько ошибок и столько парадоксов.» (Н. Х. Абель в письме к своему бывшему учителю Берндту Хольмбою, Январь 1826)

Обратимся теперь к примеру B, в котором утверждается, что:

“B” обозначает Бореля, французского математика, который работал в таких областях как теория меры и теория вероятностей. В частности, Борель связан с так называемой “теоремой о бесконечных обезьянах”, которая утверждает, что если абстрактная обезьяна будет случайным образом ударять по клавиатуре пишущей машинки на протяжении бесконечного количества времени, то вероятность того, что она напечатает некоторый конкретный текст, например, полное собрание сочинений Уильяма Шекспира, отлична от нуля.

Для того чтобы применить метод Бореля заметим, что общий член данного ряда имеет вид:

Регуляризация Бореля может быть применена к быстро расходящимся рядам в два шага. На первом шаге мы вычисляем экспоненциальную производящую функцию для последовательности членов данного ряда. Стоящий в знаменателе факториал обеспечивает сходимость данного ряд при всех значениях параметра t .

Затем мы производим преобразование Лапласа нашей экспоненциальной производящей функции и ищем его значение в точке s = 1 .

Эти шаги можно объединить, в итоге мы получим, по сути, определение суммы расходящегося ряда по Борелю .

Также мы можем использовать специализированные функции Wolfram Language для поиска экспоненциальной производящей функции и преобразования Лапласа:

При этом, ответ можно получить непосредственно с помощью Sum следующим образом.

Определение суммы по Борелю разумно, т. к. оно даёт тот же самый результат, что и обычный метод частичных сумм, если его применить к сходящемуся ряду. В этом случае можно поменять местами суммирование и интегрирование, и затем определить Гамма-функцию , при этом мы получим, что соответствующий интеграл будет равен 1 и останется просто, по сути, исходная сумма ряда:

Однако в случае с расходящимися рядами поменять местами знаки суммы и интеграла нельзя, что приводит к интересным результатам, которые даёт данный метод регуляризации.

Суммирование по Борелю представляет собой универсальный метод суммирования расходящихся рядов, который применяется, скажем, в квантовой теории поля. О применении суммирования по Борелю существует огромная коллекция литературы.

Пример C утверждает что:

“C” обозначает Чезаро (на англ. языке его фамилия пишется как Cesaro), итальянского математика, который внес значительный вклад в дифференциальную геометрию, теорию чисел и математическую физику. Чезаро был очень продуктивным математиком и написал около 80 работ в период с 1884 по 1886 г., до того, как получил степень PhD в 1887!

Для начала заметим, что общий член ряда, начиная с n = 0, имеет вид:

График показывает сильную осцилляцию частичных сумм данного ряда.

Метод Чезаро использует последовательность средних арифметических значений частичных сумм ряда для того, чтобы подавить осцилляции, что демонстрирует следующий график.

Формально говоря, суммирование по Чезаро определяется как предел последовательности средних арифметических значений частичных сумм ряда. Вычисляя данный предел для ряда из примера C, мы получим ожидаемый нами результат -1/2 (см. график выше).

Сумма по Чезаро может быть получена непосредственно, если мы в функции Sum используем данный тип регуляризации, указав соответствующее значение опции Regularization.

Метод суммирования по Чезаро играет важную роль в теории рядов Фурье , в которых ряды на основе тригонометрических функций используются для представления периодических функций. Ряд Фурье для непрерывной функции может и не сходится, но соответствующая сумма по Чезаро (или чезаровское среднее, как её обычно называют) всегда будет сходиться к функции. Этот красивый результат называется теоремой Фейера.

Наш последний пример утверждает, что сумма натурального ряда равна -1/12.

“D” означает Дирихле, немецкого математика, который совершил огромный вклад в теорию чисел и ряд других областей математики. О широте вкладов Дирихле можно судить, просто введя в Mathematica 10 следующий код.

Out//TableForm=

Регуляризация по Дирихле получила свое название от понятия “ряд Дирихле”, который определяется следующим образом:

Специальным случаем данного ряда является дзета-функция Римана , которую можно определить так:

Функция SumConvergence говорит нам, что этот ряд сходится в том случае, если действительная часть параметра s будет больше 1.

Однако, сама по себе дзета-функция Римана может быть определена и для других значений параметра s с помощью процесса аналитического продолжения, известного из теории функций комплексного переменного. Например, при s = -1, мы получим:

Но при s = -1, ряд, задающий дзета-функцию Римана и есть натуральный ряд. Отсюда мы и получаем, что:

Еще один способ осознания этого результата заключается в том, чтобы ввести бесконечно малый параметр ε в выражение члена нашего расходящегося ряда, а затем найти разложение полученной функции в ряд Маклорена с помощью функции Series , как показано ниже.

Первое слагаемое в разложении выше стремится к бесконечности при приближении параметра ε к нулю, в то же время третий член и все следующие члены стремятся к нулю. Если отбросить все члены, зависящие от ε, то оставшееся число -1/12 как раз и будет суммой по Дирихле натурального ряда. Таким образом, сумма по Дирихле получается путем отбрасывания бесконечно малых и бесконечно больших членов разложения ряда, построенного описанным нами способом. Это находится в противоречии с тем, что принято отбрасывать лишь бесконечно малые величины в обычном математическом анализе, поэтому результат суммирования расходящихся рядов по Дирихле не столь интуитивно понятен.
Стивен Хокинг применил данный метод к задаче вычисления Фейнмановых интегралов в искривленном пространстве-времени. Статья Хокинга описывает процесс дзета-регуляризации очень системно и она приобрела большую популярность после публикации.

Наши знания о расходящихся рядах основаны на глубочайших теориях, разработанных одними из лучших мыслителей последних нескольких столетий. Тем не менее, я соглашусь со многими читателям, которые как и я, чувствуют некоторое непонимание, когда они видят их в современных физических теориях. Великий Абель, вероятно, был прав, когда назвал данные ряды “изобретением дьявола”. Не исключено, что какой-то будущий Эйнштейн, обладающий умом, свободным от всяческих устоев и авторитетов, отбросит преобладающие научные убеждения и переформулирует фундаментальную физику так, что в ней не не будет места для расходящихся рядов. Но даже если такая теория станет реальностью, расходящиеся ряды все равно будут давать нам богатый источник математических идей, освещая дорогу к более глубокому пониманию нашей Вселенной.

Добавить метки

Такие суммы называются бесконечными рядами , а их слагаемые – членами ряда. (Многоточие означает, что число слагаемых бесконечно.) Решения сложных математических задач редко удается представить в точном виде посредством формул. Однако в большинстве случаев эти решения можно записать в виде рядов. После того, как такое решение найдено, методы теории рядов позволяют оценить, сколько членов ряда необходимо взять для конкретных вычислений или как записать ответ в наиболее удобном виде. Наряду с числовыми рядами мы можем рассматривать т.н. функциональные ряды , слагаемыми которых являются функции . Многие функции можно представить с помощью функциональных рядов. Изучение числовых и функциональных рядов является важной частью математического анализа .

В примерах (1) и (2) сравнительно легко догадаться, по какому закону образуются последовательные члены. Закон образования членов ряда может быть гораздо менее очевидным. Например, для ряда (3) он станет ясен, если этот ряд записать в следующем виде:

Сходящиеся ряды.

Поскольку сложение бесконечного числа членов ряда физически невозможно, необходимо определить, что именно следует понимать под суммой бесконечного ряда . Можно представить себе, что указанные операции сложения и вычитания выполняются последовательно, одна за другой, например, на компьютере. Если возникающие при этом суммы (частичные суммы) все ближе и ближе подходят к некоторому числу, то это число разумно назвать суммой бесконечного ряда. Таким образом, сумму бесконечного ряда можно определить как предел последовательности частичных сумм. При этом такой ряд называется сходящимся.

Найти сумму ряда (3) нетрудно, если заметить, что преобразованный ряд (4) можно записать в виде

Последовательные частичные суммы ряда (5) равны

и т.д.; можно заметить, что частичные суммы стремятся к 1. Таким образом, этот ряд сходится и его сумма равна 1.

В качестве примера бесконечных рядов можно рассматривать бесконечные десятичные дроби. Так, 0,353535... – это бесконечная периодическая десятичная дробь, являющаяся компактным способом записи ряда

Закон образования последовательных членов здесь понятен. Аналогично, 3,14159265... означает

но закон образования последующих членов ряда здесь неочевиден: цифры образуют десятичное разложение числа p , и трудно сразу сказать, какова, например, 100 000-я цифра, хотя теоретически эту цифру можно вычислить.

Расходящиеся ряды.

О бесконечном ряде, который не сходится, говорят, что он расходится (такой ряд называют расходящимся ). Например, ряд

расходится, так как его частичные суммы равны 1/2, 1, 1 1 / 2 , 2,.... Эти суммы не стремятся ни к какому числу как к пределу, поскольку, взяв достаточно много членов ряда, мы можем сделать частичную сумму сколь угодно большой. Ряд

также расходится, но по другой причине: частичные суммы этого ряда попеременно обращаются то в 1, то в 0 и не стремятся к пределу.

Суммирование.

Найти сумму сходящегося ряда (с заданной точностью), последовательно суммируя его члены, хотя теоретически и возможно, но практически трудно осуществимо. Например, ряд

сходится, и сумма его с точностью до десяти знаков после запятой равна 1,6449340668, но для того, чтобы вычислить ее с этой точностью, потребовалось бы взять ок. 20 млрд. членов. Такие ряды обычно суммируют, первоначально преобразуя их с помощью различных приемов. При этом используют алгебраические или вычислительные методы; например, можно показать, что сумма ряда (8) равна p 2 /6.

Обозначения.

Работая с бесконечными рядами, полезно иметь удобные обозначения. Например, конечную сумму ряда (8) можно записать как

Такая запись указывает на то, что n последовательно полагается равным 1, 2, 3, 4 и 5, а результаты складываются:

Аналогично, ряд (4) можно записать в виде

где символ Ґ указывает на то, что мы имеем дело с бесконечным рядом, а не с конечной его частью. Символ S (сигма) называют знаком суммирования.

Бесконечная геометрическая прогрессия.

Мы смогли просуммировать ряд (4), так как существовала простая формула для его частичных сумм. Аналогично, можно найти сумму ряда (2), или в общем виде,

если r принимает значения между –1 и 1. В этом случае сумма ряда (9) равна 1/(1 – r ); при других значениях r ряд (9) расходится.

Можно рассматривать периодические десятичные дроби вроде 0,353535... как иной способ записи бесконечной геометрической прогрессии

Это выражение можно записать также в виде

где в скобках стоит ряд (9) с r = 0,01; следовательно, сумма ряда (10) равна

Тем же способом можно представить в виде обычной дроби любую периодическую десятичную дробь.

Признаки сходимости.

В общем случае простой формулы для частичных сумм бесконечного ряда не существует, так что для установления сходимости или расходимости ряда прибегают к специальным методам. Например, если все члены ряда положительны, то можно показать, что ряд сходится, если каждый его член не превосходит соответствующего члена другого ряда, о котором известно, что он сходится. В принятых обозначения это можно записать следующим образом: если a n і 0 и сходится, то сходится, если 0 Ј b n Ј a n . Например, так как ряд (4) сходится и

то можно сделать вывод, что ряд (8) тоже сходится. Сравнение представляет собой основной метод, позволяющий устанавливать сходимость многих рядов, сопоставляя их с простейшими сходящимися рядами. Иногда используют более специальные признаки сходимости (их можно найти в литературе по теории рядов.) Приведем еще несколько примеров сходящихся рядов с положительными членами:

Сравнение можно использовать и для установления расходимости ряда. Если ряд расходится, то и ряд также расходится, если 0 Ј b n Ј a n .

Примерами расходящихся рядов могут служить ряды

и, в частности, т.к. гармонический ряд

В расходимости этого ряда можно убедиться, сосчитав следующие частичные суммы:

и т.д. Таким образом, частичные суммы, которые оканчиваются членами 1/4, 1/8, 1/16, 1/32, ј , превосходят частичные суммы расходящегося ряда (6), и поэтому ряд (14) должен расходиться.

Абсолютная и условная сходимости.

К таким рядам, как

метод сравнения неприменим, поскольку члены этого ряда имеют разные знаки. Если бы все члены ряда (15) были положительными, то мы получили бы ряд (3), о котором известно, что он сходится. Можно показать, что отсюда следует также сходимость ряда (15). Когда изменением знаков отрицательных членов ряда на противоположные его можно превратить в сходящийся, говорят, что исходный ряд сходится абсолютно .

Знакопеременный гармонический ряд (1) не является абсолютно сходящимся, т.к. ряд (14), состоящий из тех же, но только положительных членов, не сходится. Однако с помощью специальных признаков сходимости для знакопеременных рядов можно показать, что ряд (1) в действительности сходится. Сходящийся ряд, который не сходится абсолютно, называется условно сходящимся .

Операции с рядами.

Исходя из определения сходящегося ряда, легко показать, что его сходимость не нарушится от вычеркивания или приписывания к нему конечного числа членов, а также от умножения или деления всех членов ряда на одно и то же число (разумеется, деление на 0 исключается). При любой перестановке членов абсолютно сходящегося ряда его сходимость не нарушается, а сумма не меняется. Например, так как сумма ряда (2) равна 1, сумма ряда

также равна 1, поскольку этот ряд получается из ряда (2) перестановкой соседних членов (1-го члена со 2-м и т.д.). Можно как угодно изменять порядок следования членов абсолютно сходящегося ряда, лишь бы в новом ряду присутствовали все члены исходного. С другой стороны, перестановка членов условно сходящегося ряда может изменить его сумму и даже сделать его расходящимся. Более того, члены условно сходящегося ряда всегда можно переставить так, что он будет сходиться к любой заранее заданной сумме.

Два сходящихся ряда Sa n и Sb n можно почленно складывать (или вычитать), так что сумма нового ряда (который также сходится) складывается из сумм исходных рядов, в наших обозначениях

При дополнительных условиях, например, если оба ряда абсолютно сходятся, их можно умножать друг на друга, как это делается для конечных сумм, причем получающийся двойной ряд (см. ниже ) будет сходиться к произведению сумм исходных рядов.

Суммируемость.

Несмотря на то, что принятое нами определение сходимости бесконечного ряда кажется естественным, оно не является единственно возможным. Сумму бесконечного ряда можно определить и другими способами. Рассмотрим, например, ряд (7), который может быть записан компактно в виде

Как мы уже говорили, его частичные суммы попеременно принимают значения 1 и 0, и поэтому ряд не сходится. Но если мы образуем поочередно попарные средние его частичных сумм (текущее среднее), т.е. вычислим сначала среднее значение первой и второй частичных сумм, затем среднее второй и третьей, третьей и четвертой и т.д., то каждое такое среднее будет равно 1/2, и поэтому предел попарных средних также окажется равным 1/2. В этом случае говорят, что ряд суммируем указанным методом и его сумма равна 1/2. Было предложено много методов суммирования, позволяющих приписывать суммы довольно обширным классам расходящихся рядов и тем самым использовать некоторые расходящиеся ряды в вычислениях. Для большинства целей способ суммирования полезен, однако, только в том случае, если применительно к сходящемуся ряду он дает его конечную сумму.

Ряды с комплексными членами.

До сих пор мы молчаливо предполагали, что имеем дело лишь с действительными числами, но все определения и теоремы применимы и к рядам с комплексными числами (за исключением того, что суммы, которые могут быть получены при перестановке членов условно сходящихся рядов, не могут принимать произвольные значения).

Функциональные ряды.

Как мы уже отмечали, членами бесконечного ряда могут быть не только числа, но и функции, например,

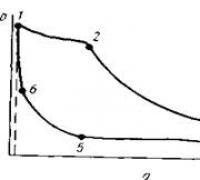
Суммой такого ряда также является функция, значение которой в каждой точке получается как предел вычисленных в этой точке частичных сумм. На рис. 1 показаны графики нескольких частичных сумм и суммы ряда (при x , изменяющемся от 0 до 1); s n (x ) означает сумму первых n членов. Сумма ряда представляет собой функцию, равную 1 при 0 Ј x x = 1. Функциональный ряд может сходиться при одних значениях x и расходиться при других; в рассмотренном нами примере ряд сходится при –1Ј x x.

Сумму функционального ряда можно понимать по-разному. В некоторых случаях важнее знать, что частичные суммы близки (в том или ином смысле) к некоторой функции на всем интервале (a , b ), чем доказывать сходимость или расходимость ряда в отдельных точках. Например, обозначив частичную сумму n -го порядка через s n (x ), мы говорим, что ряд сходится в среднем квадратичном к сумме s (x ), если

Ряд может сходиться в среднем квадратичном, даже если он не сходится ни в одной отдельной точке. Существуют также и другие определения сходимости функционального ряда.

Некоторые функциональные ряды получили название по тем функциям, которые в них входят. В качестве примера можно привести степенные ряды и их суммы:

Первый из этих рядов сходится при всех x . Второй ряд сходится при |x | r x r x| Ј 1, если r > 0 (за исключением тех случаев, когда r – неотрицательное целое число; в последнем случае ряд обрывается после конечного числа членов). Формула (17) называется биномиальным разложением для произвольной степени.

Ряды Дирихле.

Рядами Дирихле называются функциональные ряды вида S (1/a n x ), где числа a n неограниченно возрастают; примером ряда Дирихле может служить дзета-функция Римана

Ряды Дирихле часто используются в теории чисел.

Тригонометрические ряды.

Так называются функциональные ряды, содержащие тригонометрические функции; тригонометрические ряды специального вида, используемые в гармоническом анализе, называются рядами Фурье. Примером ряда Фурье может служить ряд

F (x ), обладающая следующим свойством: если мы возьмем конкретную частичную сумму ряда (18), например сумму первых трех его членов, то разность между f (x ) и этой частичной суммой, вычисленной при некотором значении x , будет мала при всех значениях x вблизи 0. Иначе говоря, хотя мы не может добиться хорошей аппроксимации функции f (x ) в какой-либо конкретной точке x , далекой от нуля, взяв даже очень много членов ряда, но при x , близком к 0, всего лишь несколько его членов дают весьма хорошее ее приближение. Такие ряды называются асимптотическими . В численных расчетах асимптотические ряды обычно полезнее, чем сходящиеся, поскольку они с помощью небольшого числа членов обеспечивают достаточно хорошее приближение. Асимптотические ряды широко используются в теории вероятностей и математической физике.

Двойные ряды.

Иногда приходится суммировать двумерные массивы чисел

Мы можем просуммировать по строкам, а затем сложить построчные суммы. Вообще говоря, у нас нет особых оснований отдавать предпочтение строкам перед столбцами, но если суммирование сначала проводить по столбцам, то результат может оказаться другим. Например, рассмотрим двойной ряд

Здесь каждая строка сходится к сумме, равной 0, и сумма построчных сумм поэтому также равна нулю. С другой стороны, сумма членов первого столбца равна 1, а всех остальных столбцов равна 0, поэтому сумма сумм по столбцам равна 1. Единственными «удобными» сходящимися двойными рядами являются абсолютно сходящиеся двойные ряды: их можно суммировать по строкам или столбцам, равно как и любым другим способом, и сумма всегда получается одной и той же. Какого-либо естественного определения условной сходимости двойных рядов не существует.

На практике часто не столь важно найти сумму ряда, как ответить на вопрос о сходимости ряда. Для этой цели используются признаки сходимости, основанные на свойствах общего члена ряда.

Необходимый признак сходимости ряда

ТЕОРЕМА 1

Если ряд сходится, то его общий член стремится к нулю при
, т.е.
.

Кратко : если ряд сходится, то его общий член стремится к нулю.

Доказательство. Пусть ряд сходится и его сумма равна . Для любого частичная сумма

.

Тогда . 

Из доказанного необходимого признака сходимости вытекает достаточный признак расходимости ряда: если при
общий член ряда не стремится к нулю, то ряд расходится.

Пример 4.

Для этого ряда общий член
и
.

Следовательно, данный ряд расходится.

Пример 5. Исследовать на сходимость ряд

Очевидно, что общий член этого ряда, вид которого не указан ввиду громоздкости выражения, стремится к нулю при
, т.е. необходимый признак сходимости ряда выполняется, однако этот ряд расходится, так как его сумма стремится к бесконечности.

Знакоположительные числовые ряды

Числовой ряд, все члены которого положительны, называется знакоположительным.

ТЕОРЕМА 2 (Критерий сходимости знакоположительного ряда)

Для сходимости знакоположительного ряда необходимо и достаточно, чтобы все его частичные суммы были ограничены сверху одним и тем же числом.

Доказательство. Так как для любого
, то, т.е. последовательность
– монотонно возрастающая, поэтому для существования предела необходимо и достаточно ограничение последовательности сверху каким-либо числом.

Эта теорема в большей степени имеет теоретическое, чем практическое значение. Далее приведены другие признаки сходимости, имеющие большее применение.

Достаточные признаки сходимости знакоположительных рядов

ТЕОРЕМА 3 (Первый признак сравнения)

Пусть даны два знакоположительных ряда:

(1)

(2)

причем, начиная с некоторого номера
, для любого
выполняется неравенство
Тогда:

Схематическая запись первого признака сравнения:

сход.сход.

расх.расх.

Доказательство. 1) Так как отбрасывание конечного числа членов ряда не влияет на его сходимость, докажем теорему для случая
. Пусть для любого
имеем

, (3)

где
и
- соответственно частичные суммы рядов (1) и (2).

Если ряд (2) сходится, то существует число
. Поскольку при этом последовательность
- возрастающая, ее предел больше любого из ее членов, т.е.
для любого . Отсюда из неравенства (3) следует
. Таким образом, все частичные суммы ряда (1) ограничены сверху числом . Согласно теореме 2 этот ряд сходится.

2) Действительно, если бы ряд (2) сходился, то по признаку сравнения сходился бы и ряд (1). 

Для применения этого признака часто используют такие ряды-эталоны, сходимость или расходимость которых известна заранее, например:

3) - ряд Дирихле (он сходится при
и расходится при
).

Кроме этого часто используют ряды, которые можно получить с помощью следующих очевидных неравенств:

,

,
,
.

Рассмотрим на конкретных примерах схему исследования знакоположительного ряда на сходимость с помощью первого признака сравнения.

Пример 6. Исследовать ряд
на сходимость.

Шаг 1. Проверим знакоположительность ряда:
для

Шаг 2. Проверим выполнение необходимого признака сходимости ряда:
. Так как
, то

(если вычисление предела вызывает трудности, то этот шаг можно пропустить).

Шаг 3. Используем первый признак сравнения. Для этого подберем для данного ряда ряд-эталон. Так как
, то в качестве эталона можно взять ряд
, т.е. ряд Дирихле. Этот ряд сходится, так как показатель степени
. Следовательно, согласно первому признаку сравнения сходится и исследуемый ряд.

Пример 7. Исследовать ряд
на сходимость.

1) Данный ряд знакоположительный, так как
для

2) Необходимый признак сходимости ряда выполняется, ибо

3) Подберем ряд-эталон. Так как
, то в качестве эталона можно взять геометрический ряд

. Этот ряд сходится, следовательно, сходится и исследуемый ряд.

ТЕОРЕМА 4 (Второй признак сравнения)

Если для знакоположительных рядов и существует отличный от нуля конечный предел
, то ряды сходятся или расходятся одновременно.

Доказательство. Пусть ряд (2) сходится; докажем, что тогда сходится и ряд (1). Выберем какое-нибудь число , большее, чем . Из условия
вытекает существование такого номера , что для всех
справедливо неравенство
, или, что то же,

(4)

Отбросив в рядах (1) и (2) первые членов (что не влияет на сходимость), можно считать, что неравенство (4) справедливо для всех
Но ряд с общим членом
сходится в силу сходимости ряда (2). Согласно первому признаку сравнения, из неравенства (4) следует сходимость ряда (1).

Пусть теперь сходится ряд (1); докажем сходимость ряда (2). Для этого следует просто поменять ролями заданные ряды. Так как

то, по доказанному выше, из сходимости ряда (1) должна следовать сходимость ряда (2). 

Если
при
(необходимый признак сходимости), то из условия
, следует, чтои– бесконечно малые одного порядка малости (эквивалентные при
). Следовательно, если дан ряд , где
при
, то для этого ряда можно брать ряд-эталон , где общий член имеет тот же порядок малости, что и общий член данного ряда.

При выборе ряда-эталона можно пользоваться следующей таблицей эквивалентных бесконечно малых при
:

1)
; 4)
;

2)
; 5)
;

3)
; 6)
.

Пример 8. Исследовать на сходимость ряд

.

для любого
.

Так как
, то возьмем в качестве ряда-эталона гармонический расходящийся ряд
. Поскольку предел отношения общих членовиконечен и отличен от нуля (он равен 1), то на основании второго признака сравнения данный ряд расходится.

Пример 9.
по двум признакам сравнения.

Данный ряд знакоположительный, так как
, и
. Поскольку
, то в качестве ряда-эталона можно брать гармонический ряд. Этот ряд расходится и следовательно, по первому признаку сравнения, исследуемый ряд также расходится.

Так как для данного ряда и ряда-эталона выполняется условие
(здесь использован 1-й замечательный предел), то на основании второго признака сравнения ряд
– расходится.

ТЕОРЕМА 5 (Признак Даламбера)

существует конечный предел
, то ряд сходится при
и расходится при
.

Доказательство. Пусть
. Возьмем какое-либо число, заключенное между и 1:
. Из условия
следует, что начиная с некоторого номера выполняется неравенство

;
;
(5)

Рассмотрим ряд

Согласно (5) все члены ряда (6) не превосходят соответствующих членов бесконечной геометрической прогрессии
Поскольку
, эта прогрессия является сходящейся. Отсюда в силу первого признака сравнения вытекает сходимость ряда

Случай
рассмотрите самостоятельно.

Замечания :

следует, что остаток ряда

.

Признак Даламбера удобен на практике тогда, когда общий член ряда содержит показательную функцию или факториал.

Пример 10. Исследовать на сходимость ряд по признаку Даламбера.

Данный ряд знакоположительный и

.

(Здесь при вычислении дважды применено правило Лопиталя).

то по признаку Даламбера данный ряд сходится.

Пример 11. .

Данный ряд знакоположительный и
. Поскольку

то данный ряд сходится.

ТЕОРЕМА 6 (Признак Коши)

Если для знакоположительного ряда существует конечный предел
, то при
ряд сходится, а при
ряд расходится.

Доказательство аналогично теореме 5.

Замечания :

Пример 12. Исследовать на сходимость ряд
.

Данный ряд знакоположительный, так как
для любого
. Поскольку вычисление предела
вызывает определенные трудности, то проверку выполнимости необходимого признака сходимости ряда опускаем.

то по признаку Коши данный ряд расходится.

ТЕОРЕМА 7 (Интегральный признак сходимости Маклорена - Коши)

Пусть дан ряд

члены которого положительны и не возрастают:

Пусть, далее
- функция, которая определена для всех вещественных
, непрерывна, не возрастает и

ВВЕДЕНИЕ

Методическое пособие предназначено для преподавателей математики в техникумах, а также для студентов второго курса, всех специальностей.

В данной работе излагаются основные понятия теории рядов. Теоретический материал соответствует требованиям Государственного образовательного стандарта среднего профессионального образования (Министерство образования Российской Федерации. М., 2002г.).

Изложение теоретического материала по всей теме сопровождается рассмотрением большого количества примеров и задач, ведется на доступном, по-возможности строгом языке. В конце пособия приведены примеры и задания, которые студенты могут выполнять в режиме самоконтроля.

Пособие предназначено для студентов заочной и дневной форм обучения.

Учитывая уровень подготовки учащихся техникума, а также крайне ограниченное число часов (12 часов + 4 ф.), отводимое программой для прохождения высшей математики в техникумах, строгие выводы, представляющие большие трудности для усвоения, опущены, ограничиваясь рассмотрением примеров.

ОСНОВНЫЕ ПОНЯТИЯ

Решение задачи, представленной в математических терминах, например, в виде комбинации различных функций, их производных и интегралов, нужно уметь “довести до числа”, которое чаще всего и служит окончательным ответом. Для этого в различных разделах математики выработаны различные методы.

Раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией рядов.

Даже если некоторые тонкие понятия математического анализа появились вне связи с теорией рядов, они немедленно применялись к рядам, которые служили как бы инструментом для испытания значимости этих понятий. Такое положение сохраняется и сейчас.

Выражение вида

где ;;;…;;… - члены ряда; - n-ый или общий член ряда, называется бесконечным рядом (рядом).

Если члены ряда:

I. Числовой ряд

1.1. Основные понятия числового ряда.

Числовым рядом называется сумма вида

, (1.1)

где ,,,…,,…, называемые членами ряда, образуют бесконечную последовательность; членназывается общим членом ряда.

составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм .

Если при бесконечном возрастании номера n частичная сумма ряда стремится к пределу, то ряд называется сходящимся, а число - суммой сходящегося ряда, т.е.

Эта запись равносильна записи

.

Если частичная сумма ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к или ), то такой ряд называется расходящимся .

Если ряд сходящийся , то значение при достаточно большом n является приближенным выражением суммы ряда S .

Разность называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е., и наоборот, если остаток стремится к нулю, то ряд сходится.

1.2. Примеры числовых рядов.

Пример 1. Ряд вида

(1.2)

называется геометрическим .

Геометрический ряд образован из членов геометрической прогрессии.

Известно, что сумма её первых n членов . Очевидно: это n- ая частичная сумма ряда (1.2).

Возможны случаи:

Ряд (1.2) принимает вид:

,ряд расходится;

Ряд (1.2) принимает вид:

Не имеет предела, ряд расходится.

- конечное число, ряд сходится.

- ряд расходится.

Итак, данный ряд сходится при и расходится при .

Пример 2. Ряд вида

(1.3)

называется гармоническим .

Запишем частичную сумму этого ряда:

Сумма больше суммы, представленной следующим образом:

или .

Если , то , или .

Следовательно, если , то , т.е. гармонический ряд расходится.

Пример 3. Ряд вида

(1.4)

называется обобщенным гармоническим .

Если , то данный ряд обращается в гармонический ряд, который является расходящимся.

Если , то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При имеем геометрический ряд, в котором ; он является сходящимся.

Итак, обобщенный гармонический ряд сходится при и расходится при .

1.3. Необходимый и достаточные признаки сходимости.

Необходимый признак сходимости ряда.

Ряд может сходиться только при условии, что его общий член при неограниченном увеличении номера стремится к нулю: .

Если , то ряд расходится – это достаточный признак расходимости ряда.

Достаточные признаки сходимости ряда с положительными членами.

Признак сравнения рядов с положительными членами.

Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого, заведомо сходящегося ряда; исследуемый ряд расходится, если его члены превосходят соответствующие члены другого, заведомо расходящегося ряда.

Признак Даламбера.

Если для ряда с положительными членами

выполняется условие , то ряд сходится при и расходится при .

Признак Даламбера не дает ответа, если . В этом случае для исследования ряда применяются другие приемы.

Упражнения.

Записать ряд по его заданному общему члену:

Полагая ,,,…, имеем бесконечную последовательность чисел:

Сложив его члены, получим ряд

.

Поступая так же, получим ряд

.

Придаваязначения 1,2,3,… и учитывая, что,,,…, получим ряд

.

Найти n- ый член ряда по его данным первым членам:

Знаменатели членов ряда, начиная с первого, являются четными числами; следовательно, n- ый член ряда имеет вид .

Числители членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, начиная с 3. Знаки чередуются по закону или по закону . Значит, n- й член ряда имеет вид . или .

Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:

;

.

Находим .

Необходимый признак сходимости ряда выполняется, но для решения вопроса о сходимости нужно применить один из достаточных признаков сходимости. Сравним данный ряд с геометрическим рядом

,

который сходится, так как.

Сравнивая члены данного ряда, начиная со второго, с соответствующими членами геометрического ряда, получим неравенства

т.е. члены данного ряда, начиная со второго, соответственно меньше членов геометрического ряда, откуда следует, что данный ряд сходится.

.

Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.

Находим .

Необходимый признак сходимости ряда выполняется. Сравним данный ряд с обобщенным гармоническим рядом

,

который сходится, поскольку, следовательно, сходится и данный ряд.

Исследовать сходимость ряда, используя признак Даламбера:

;

.

Подставив в общий член ряда вместо n число n+ 1, получим . Найдем предел отношения -го члена к n- му члену при :

Следовательно, данный ряд сходится.

Значит, данный ряд расходится.

Т.е. ряд расходится.

II. Знакопеременный ряд

2.1 Понятие знакопеременного ряда.

Числовой ряд

называется знакопеременным , если среди его членов имеются как положительные, так и отрицательные числа.

Числовой ряд называется знакочередующимся , если любые два стоящие рядом члена имеют противоположные знаки.

где для всех (т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно). Например,

;

;

.

Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714г. Лейбницем в письме к И.Бернулли).

2.2 Признак Лейбница. Абсолютная и условная сходимость ряда.

Теорема (Признак Лейбница).

Знакочередующийся ряд сходится, если:

Последовательность абсолютных величин членов ряда монотонно убывает, т.е. ;

Общий член ряда стремится к нулю:.

При этом сумма S ряда удовлетворяет неравенствам

Замечания.

Исследование знакочередующегося ряда вида

(с отрицательным первым членом) сводится путем умножения всех его членов на к исследованию ряда .

Ряды, для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница).

Соотношение позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой .

Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд , сумма которого по модулю меньше первого члена этого ряда, т.е.. Поэтому ошибка меньше модуля первого из отброшенных членов.

Пример. Вычислить приблизительно сумму ряда .

Решение: данный ряд Лейбницевского типа. Он сходится. Можно записать:

.

Взяв пять членов, т.е. заменивна

Сделаем ошибку, меньшую,

чем. Итак,.

Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема. Пусть дан знакопеременный ряд

Если сходится ряд

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Признак сходимости Лейбница для знакочередующихся рядов служит достаточным признаком сходимости знакочередующихся рядов.

Знакопеременный ряд называется абсолютно сходящимся , если сходится ряд, составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.

Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно (неабсолютно) сходящимся.

2.3. Упражнения.

Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:

и

Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.

Ряд , составленный из абсолютных величин данного ряда, является гармоническим рядом, который, расходится. Поэтому данный ряд сходится условно.

Члены данного ряда по абсолютной величине монотонно убывают:

, но

.

Ряд расходится, так как признак Лейбница не выполняется.

Используя признак Лейбница, получим

;,

т.е. ряд сходится.

.

Это геометрический ряд вида, где, который сходится. Поэтому данный ряд сходится абсолютно.

Используя признак Лейбница, имеем

;

, т.е. ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

, или

.

Это обобщенный гармонический ряд, который расходится, так как. Следовательно, данный ряд сходится условно.

III. Функциональный ряд

3.1. Понятие функционального ряда.

Ряд, членами которого являются функции от , называется функциональным :

Придавая определенное значение , получим числовой ряд

который может быть как сходящимся, так и расходящимся.

Если полученный числовой ряд сходится, то точка называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда.

Совокупность числовых значений аргумента , при которых функциональный ряд сходится, называется его областью сходимости .

В области сходимости функционального ряда его сумма является некоторой функцией от :.

Определяется она в области сходимости равенством

, где

Частичная сумма ряда.

Пример. Найти область сходимости ряда .

Решение. Данный ряд является рядом геометрической прогрессии со знаменателем . Следовательно, этот ряд сходится при , т.е. при всех ; сумма ряда равна ;

, при .

3.2. Степенные ряды.

Степенным рядом называется ряд вида

,

где числа называются коэффициентами ряда , а член - общим членом ряда.

Областью сходимости степенного ряда называется множество всех значений , при которых данный ряд сходится.

Число называется радиусом сходимости степенного ряда, если при ряд сходится и притом абсолютно, а при ряд расходится.

Радиус сходимости найдем, используя признак Даламбера:

(не зависит от),

т.е. если степенной ряд сходится при любых , удовлетворяющих данному условию и расходится при .

Отсюда следует, что если существует предел

,

то радиус сходимости рядаравен этому пределу и степенной ряд сходится при , т.е. в промежутке , который называется промежутком (интервалом) сходимости.

Если , то степенной ряд сходится в единственной точке .

На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.

Сходимость степенного ряда при и исследуется с помощью какого-либо из признаков сходимости.

3.3. Упражнения.

Найти область сходимости ряда:

Решение. Найдем радиус сходимости данного ряда:

.

Следовательно, данный ряд абсолютно сходится на всей числовой оси.

Решение. Воспользуемся признаком Даламбера. Для данного ряда имеем:

.

Ряд абсолютно сходится, если или . Исследуем поведение ряда на концах интервала сходимости.

При имеем ряд

При имеем ряд- это тоже сходящийся Лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок.

Решение. Найдем радиус сходимости ряда:

Следовательно, ряд сходится при, т.е. при.

Приимеем ряд, который сходится по признаку Лейбница.

Приимеем расходящийся ряд

.

Следовательно, областью сходимости исходного ряда является промежуток.

IV. Разложение элементарных функций в ряд Маклорена.

Для приложений важно уметь данную функцию разлагать в степенной ряд, т.е. функцию представлять в виде суммы степенного ряда.

Рядом Тейлора для функции называется степенной ряд вида

Если , то получим частный случай ряда Тейлора

который называется рядом Маклорена .

Степенной ряд внутри его промежутка сходимости можно почленно дифференцировать и интегрировать сколько угодно раз, причем полученные ряды имеют тот же промежуток сходимости, что и исходный ряд.

Два степенных ряда можно почленно складывать и умножать по правилам сложения и умножения многочленов. При этом промежуток сходимости полученного нового ряда совпадает с общей частью промежутков сходимости исходных рядов.

Для разложения функции в ряд Маклорена необходимо:

Вычислить значения функции и ее последовательных производных в точке , т.е.,,,…,;

Составить ряд Маклорена, подставив значения функции и ее последовательных производных в формулу ряда Маклорена;

Найти промежуток сходимости полученного ряда по формуле

, .

Пример 1. Разложить в ряд Маклорена функцию.

Решение. Так как , то, заменяя на в разложении , получим:

Пример 2. Выписать ряд Маклорена функции .

Решение. Так как , то воспользовавшись формулой , в которой заменим на , получим:

,

Пример 3. Разложить в ряд Маклорена функцию .

Решение. Воспользуемся формулой . Так как

, то заменивнаполучим:

, или

где , т.е. .

V. Практические задания для самоконтроля студентов.

При помощи признака сравнения рядов установить сходимость

или расходимость рядов:

cходится условно;

cходится условно;

cходится абсолютно.

;

;

VII. Историческая справка.

Решение многих задач сводится к вычислению значений функций и интегралов или к решению дифференциальных уравнений, содержащих производные или дифференциалы неизвестных функций.

Однако точное выполнение указанных математических операций во многих случаях оказывается весьма затруднительным или невозможным. В этих случаях можно получить приближенное решение многих задач с любой желаемой точностью при помощи рядов.

Ряды представляют собой простой и совершенный инструмент математического анализа для приближенного вычисления функций, интегралов и решений дифференциальных уравнений.

И стоящим справа функциональным рядом.

Для того, чтобы вместо знака “” можно было поставить знак равенства, необходимо провести некоторые дополнительные рассуждения, связанные именно с бесконечностью числа слагаемых в правой части равенства и касающиеся области сходимости ряда.

При формула Тейлора принимает вид, в котором называется формулой Маклорена:

Колин Маклорен (1698 – 1746), ученик Ньютона, в работе “Трактат о флюксиях” (1742) установил, что степенной ряд, выражающий аналитическую функцию, - единственный, и это будет ряд Тейлора, порожденный такой функцией. В формуле бинома Ньютона коэффициенты при степенях представляют собой значения , где .

Итак, ряды возникли в XVIII в. как способ представления функций, допускающих бесконечное дифференцирование. Однако функция, представляемая рядом, не называлась его суммой, и вообще в то время не было еще определено, что такое сумма числового или функционального ряда, были только попытки ввести это понятие.

Например, Л. Эйлер (1707-1783), выписав для функции соответствующий ей степенной ряд, придавал переменной конкретное значение . Получался числовой ряд. Суммой этого ряда Эйлер cчитал значение исходной функции в точке . Но это не всегда верно.

О том, что расходящийся ряд не имеет суммы, ученые стали догадываться только в XIX в., хотя в XVIII в. многие, и прежде всего Л. Эйлер, много работали над понятиями сходимости и расходимости. Эйлер называл ряд сходящимся, если его общий член стремится к нулю при возрастании .

В теории расходящихся рядов Эйлер получил немало существенных результатов, однако результаты эти долго не находили применения. Еще в 1826г. Н.Г. Абель (1802 – 1829) называл расходящиеся ряды “дьявольским измышлением”. Результаты Эйлера нашли обоснование лишь в конце XIX в.

В формировании понятия суммы сходящегося ряда большую роль сыграл французский ученый О.Л. Коши (1789 – 1857); он сделал чрезвычайно много не только в теории рядов, но и теории пределов, в разработке самого понятия предела. В 1826г. Коши заявил, что расходящийся ряд не имеет суммы.

В 1768г. французский математик и философ Ж.Л. Д’Аламбер исследовал отношение последующего члена к предыдущему в биномиальном ряде и показал, что если это отношение по модулю меньше единицы, то ряд сходится. Коши в 1821г. доказал теорему, излагающую в общем виде признак сходимости знакоположительных рядов, называемых теперь признаком Д’Аламбера.

Для исследования сходимости знакочередующихся рядов используется признак Лейбница.

Г.В. Лейбниц (1646 – 1716), великий немецкий математик и философ, наряду с И. Ньютоном является основоположником дифференциального и интегрального исчисления.

Список литературы:

Основная:

1. Богомолов Н.В., Практические занятия по математике. М., “Высшая школа”, 1990 – 495 с.;
2. Тарасов Н.П., Курс высшей математики для техникумов. М., “Наука”, 1971 – 448 с.;
3. Зайцев И.Л., Курс высшей математики для техникумов. М., государственное издательство техникумов – теоретической литературы, 1957 - 339 с.;
4. Письменный Д.Т., Курс лекций по высшей математике. М., “Айрис Пресс”, 2005, часть 2 – 256 с.;
5. Выгодский М.Я., Справочник по высшей математике. М., “Наука”, 1975 – 872 с.;

Дополнительная:

1. Гусак А.А., Высшая математика. В 2-х т., Т.2: Учебное пособие для студентов вузов. Мос., “ТетраСистемс”, 1988 – 448 с.;
2. Григулецкий В.Г., Лукьянова И.В., Петунина И.А., Математика для студентов экономических специальностей. Часть 2. Краснодар, 2002 – 348 с.;
3. Григулецкий В.Г. и др. Задачник-практикум по математике. Краснодар. КГАУ, 2003 – 170 с.;
4. Григулецкий В.Г., Степанцова К.Г., Гетман В.Н., Задачи и упражнения для студентов учетно-финансового факультета. Краснодар. 2001 – 173 с.;
5. Григулецкий В.Г., Ященко З.В., Высшая математика. Краснодар, 1998 – 186 с.;
6. Малыхин В.И., Математика в экономике. М., “Инфра-М”, 1999 – 356с.

Вам могут быть интересны следующие материалы

Розетки 

Провода и кабели

Заземление

Инструменты

Источники света

Светильники

© 2024 Helperlife - Строительный портал